题目
设 alpha (alpha )_(1),(alpha )_(2),(alpha )_(3),(beta )_(1),(beta )_(2) 均为四维列向量矩阵，alpha (alpha )_(1),(alpha )_(2),(alpha )_(3),(beta )_(1),(beta )_(2)且 alpha (alpha )_(1),(alpha )_(2),(alpha )_(3),(beta )_(1),(beta )_(2) ，则 alpha (alpha )_(1),(alpha )_(2),(alpha )_(3),(beta )_(1),(beta )_(2)____( A ) -8 ( B ) -16 ( C ) 16 ( D ) 8
设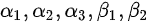 
均为四维列向量矩阵，
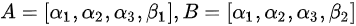且 
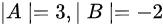，则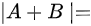 
____
( A ) -8
( B ) -16
( C ) 16
( D ) 8
题目解答
答案
由题设可知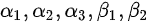 均为四维列向量矩阵，且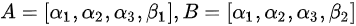
则根据行列式的性质：（1）若某行（列）含有公因子，则可将公因子提出行列式之外；（2）若某行（列）的元素为两个元素之和，则可拆分成两个行列式之和；可知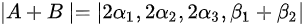
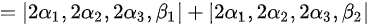
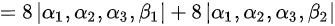
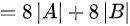
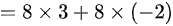
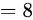
故答案为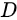
。
解析
步骤 1：理解行列式性质
行列式具有以下性质：若某行（列）含有公因子，则可将公因子提出行列式之外；若某行（列）的元素为两个元素之和，则可拆分成两个行列式之和。
步骤 2：计算 |A+B|
根据行列式的性质，$|A+B|=|2{a}_{1},2{a}_{2},2{a}_{3},{\beta }_{1}+{\beta }_{2}|$，可以拆分成$|2{a}_{1},2{a}_{2},2{a}_{3},{\beta }_{1}|+|2{a}_{1},2{a}_{2},2{a}_{3},{\beta }_{2}|$。
步骤 3：提取公因子
由于每列都有公因子2，可以将2提出行列式之外，得到$8|{a}_{1},{a}_{2},{a}_{3},{\beta }_{1}|+8|{a}_{1},{a}_{2},{a}_{3},{\beta }_{2}|$。
步骤 4：代入已知行列式值
根据已知条件，$|A|=3$，$|B|=-2$，代入上式得到$8|A|+8|B|=8\times 3+8\times (-2)=8$。
行列式具有以下性质：若某行（列）含有公因子，则可将公因子提出行列式之外；若某行（列）的元素为两个元素之和，则可拆分成两个行列式之和。
步骤 2：计算 |A+B|
根据行列式的性质，$|A+B|=|2{a}_{1},2{a}_{2},2{a}_{3},{\beta }_{1}+{\beta }_{2}|$，可以拆分成$|2{a}_{1},2{a}_{2},2{a}_{3},{\beta }_{1}|+|2{a}_{1},2{a}_{2},2{a}_{3},{\beta }_{2}|$。
步骤 3：提取公因子
由于每列都有公因子2，可以将2提出行列式之外，得到$8|{a}_{1},{a}_{2},{a}_{3},{\beta }_{1}|+8|{a}_{1},{a}_{2},{a}_{3},{\beta }_{2}|$。
步骤 4：代入已知行列式值
根据已知条件，$|A|=3$，$|B|=-2$，代入上式得到$8|A|+8|B|=8\times 3+8\times (-2)=8$。