题目
求内接于半径为R的球且有最大体积的长方体。
求内接于半径为R的球且有最大体积的长方体。
题目解答
答案
设长方体的长宽高分别为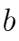
，
，
，
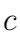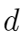长方体内接于半径为R的球，
可得$$\sqrt{b^2+c^2+d^2}=2R$$，即$$b^2+c^2+d^2=4R^2$$
$$\frac{b^2+c^2+d^2}{3}\geqslant \root3\of{b^2c^2d^2}$$，当且仅当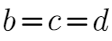
时成立，
长方体的体积为$$V=bcd\leqslant (\frac{b^2+c^2+d^2}{3})^\frac{3}{2}$$$$=(\frac{4R^2}{3})^\frac{3}{2}$$$$=\frac{8\sqrt{3}}{9}R^3$$，当且仅当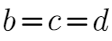$$=\frac{2\sqrt{3}}{3}R$$时成立，
此长方体的长宽高都是$$ \frac{2\sqrt{3}}{3}R$$.
解析
步骤 1：确定长方体的长宽高
设长方体的长宽高分别为 $b$，$c$，$d$。
步骤 2：利用球的半径和长方体的对角线关系
长方体内接于半径为 $R$ 的球，可得长方体的对角线等于球的直径，即
$$\sqrt{b^2+c^2+d^2}=2R$$
从而得到
$$b^2+c^2+d^2=4R^2$$
步骤 3：利用均值不等式求体积的最大值
根据均值不等式，有
$$\frac{b^2+c^2+d^2}{3}\geqslant \sqrt[3]{b^2c^2d^2}$$
当且仅当 $b=c=d$ 时成立。
长方体的体积为
$$V=bcd\leqslant \left(\frac{b^2+c^2+d^2}{3}\right)^{\frac{3}{2}}$$
$$=\left(\frac{4R^2}{3}\right)^{\frac{3}{2}}$$
$$=\frac{8\sqrt{3}}{9}R^3$$
当且仅当 $b=c=d=\frac{2\sqrt{3}}{3}R$ 时成立。
设长方体的长宽高分别为 $b$，$c$，$d$。
步骤 2：利用球的半径和长方体的对角线关系
长方体内接于半径为 $R$ 的球，可得长方体的对角线等于球的直径，即
$$\sqrt{b^2+c^2+d^2}=2R$$
从而得到
$$b^2+c^2+d^2=4R^2$$
步骤 3：利用均值不等式求体积的最大值
根据均值不等式，有
$$\frac{b^2+c^2+d^2}{3}\geqslant \sqrt[3]{b^2c^2d^2}$$
当且仅当 $b=c=d$ 时成立。
长方体的体积为
$$V=bcd\leqslant \left(\frac{b^2+c^2+d^2}{3}\right)^{\frac{3}{2}}$$
$$=\left(\frac{4R^2}{3}\right)^{\frac{3}{2}}$$
$$=\frac{8\sqrt{3}}{9}R^3$$
当且仅当 $b=c=d=\frac{2\sqrt{3}}{3}R$ 时成立。