题目
4.已知实数x满足 ^2+dfrac (1)({x)^2}-3x-dfrac (3)(x)+2=0, 求 ^3+dfrac (1)({x)^3} 的值.
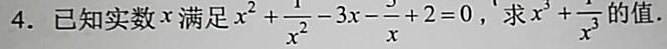
题目解答
答案
本题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．
已知等式变形后，利用完全平方公式化简，利用非负数的性质求出x的值，代入原式计算即可得到结果．
${x}^{2}+\dfrac {1} {{x}^{2}}-3x-\dfrac {3} {x}+2=0$
$\left ( {x+\dfrac {1} {x}} \right )^{2}-2-3\left ( {x+\dfrac {1} {x}} \right )+2=0$
$\left ( {x+\dfrac {1} {x}} \right )^{2}-3\left ( {x+\dfrac {1} {x}} \right )=0$
$\left ( {x+\dfrac {1} {x}} \right )\left ( {x+\dfrac {1} {x}-3} \right )=0$
$\therefore x+\dfrac {1} {x}=0$或$x+\dfrac {1} {x}-3=0$
$\therefore x+\dfrac {1} {x}=0$或$x+\dfrac {1} {x}=3$
当$x+\dfrac {1} {x}=0$时，${x}^{3}+\dfrac {1} {{x}^{3}}=\left ( {x+\dfrac {1} {x}} \right )\left ( {{x}^{2}-1+\dfrac {1} {{x}^{2}}} \right )=0$
当$x+\dfrac {1} {x}=3$时，${x}^{3}+\dfrac {1} {{x}^{3}}=\left ( {x+\dfrac {1} {x}} \right )\left ( {{x}^{2}-1+\dfrac {1} {{x}^{2}}} \right )=3\left [ {\left ( {x+\dfrac {1} {x}} \right )^{2}-3} \right ]=3\times \left ( {{3}^{2}-3} \right )=18$
$\therefore {x}^{3}+\dfrac {1} {{x}^{3}}$的值为$0$或$18$
已知等式变形后，利用完全平方公式化简，利用非负数的性质求出x的值，代入原式计算即可得到结果．
${x}^{2}+\dfrac {1} {{x}^{2}}-3x-\dfrac {3} {x}+2=0$
$\left ( {x+\dfrac {1} {x}} \right )^{2}-2-3\left ( {x+\dfrac {1} {x}} \right )+2=0$
$\left ( {x+\dfrac {1} {x}} \right )^{2}-3\left ( {x+\dfrac {1} {x}} \right )=0$
$\left ( {x+\dfrac {1} {x}} \right )\left ( {x+\dfrac {1} {x}-3} \right )=0$
$\therefore x+\dfrac {1} {x}=0$或$x+\dfrac {1} {x}-3=0$
$\therefore x+\dfrac {1} {x}=0$或$x+\dfrac {1} {x}=3$
当$x+\dfrac {1} {x}=0$时，${x}^{3}+\dfrac {1} {{x}^{3}}=\left ( {x+\dfrac {1} {x}} \right )\left ( {{x}^{2}-1+\dfrac {1} {{x}^{2}}} \right )=0$
当$x+\dfrac {1} {x}=3$时，${x}^{3}+\dfrac {1} {{x}^{3}}=\left ( {x+\dfrac {1} {x}} \right )\left ( {{x}^{2}-1+\dfrac {1} {{x}^{2}}} \right )=3\left [ {\left ( {x+\dfrac {1} {x}} \right )^{2}-3} \right ]=3\times \left ( {{3}^{2}-3} \right )=18$
$\therefore {x}^{3}+\dfrac {1} {{x}^{3}}$的值为$0$或$18$
解析
步骤 1：化简已知等式
已知等式为 ${x}^{2}+\dfrac {1}{{x}^{2}}-3x-\dfrac {3}{x}+2=0$，我们首先尝试将等式中的项进行分组，以便于后续的化简。
步骤 2：利用完全平方公式
将等式中的 ${x}^{2}+\dfrac {1}{{x}^{2}}$ 项和 $-3x-\dfrac {3}{x}$ 项分别进行分组，利用完全平方公式进行化简。
步骤 3：求解 $x+\dfrac {1}{x}$
通过化简后的等式，求解出 $x+\dfrac {1}{x}$ 的值。
步骤 4：求解 ${x}^{3}+\dfrac {1}{{x}^{3}}$
利用 $x+\dfrac {1}{x}$ 的值，求解 ${x}^{3}+\dfrac {1}{{x}^{3}}$ 的值。
已知等式为 ${x}^{2}+\dfrac {1}{{x}^{2}}-3x-\dfrac {3}{x}+2=0$，我们首先尝试将等式中的项进行分组，以便于后续的化简。
步骤 2：利用完全平方公式
将等式中的 ${x}^{2}+\dfrac {1}{{x}^{2}}$ 项和 $-3x-\dfrac {3}{x}$ 项分别进行分组，利用完全平方公式进行化简。
步骤 3：求解 $x+\dfrac {1}{x}$
通过化简后的等式，求解出 $x+\dfrac {1}{x}$ 的值。
步骤 4：求解 ${x}^{3}+\dfrac {1}{{x}^{3}}$
利用 $x+\dfrac {1}{x}$ 的值，求解 ${x}^{3}+\dfrac {1}{{x}^{3}}$ 的值。