题目
例1 计算 (int )_(1)sqrt ({x)^2+(y)^2}ds, 其中L为圆周 ^2+(y)^2=4x.
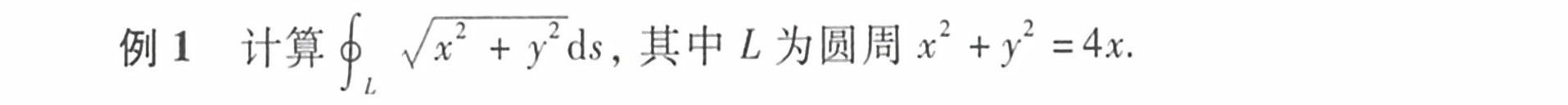
题目解答
答案

解析
步骤 1:确定圆周的方程
圆周的方程为 ${x}^{2}+{y}^{2}=4x$,可以改写为 $(x-2)^2 + y^2 = 4$,这是一个以 $(2,0)$ 为圆心,半径为 $2$ 的圆。
步骤 2:利用直角坐标方程进行计算
由方程 ${x}^{2}+{y}^{2}=4x$ 知,$2x+2yy'=4$,得 $y'=\dfrac {2-x}{y}$。于是 $ds=\sqrt {1+{y'}^{2}}dx=\dfrac {2}{\sqrt {{y}^{2}}}dx=\dfrac {2}{\sqrt {4x-{x}^{2}}}dx$。则 ${\int }_{1}\sqrt {{x}^{2}+{y}^{2}}ds=2{\int }_{0}^{4}\sqrt {4x}\dfrac {2}{\sqrt {4x-{x}^{2}}}dx=8{\int }_{0}^{2}\dfrac {dx}{\sqrt {4-x}}=32$。
步骤 3:利用参数方程进行计算
圆周 ${x}^{2}+{y}^{2}=4x$ 的参数方程为 $\left\{\begin{array}{l}x=2+2\cos t\\y=2\sin t\end{array}\right.$,$0\leq t\leq 2\pi$。则 $ds=2dt$,$\sqrt {{x}^{2}+{y}^{2}}ds=2{\int }_{0}^{2\pi }\sqrt {8(1+\cos t)}dt=8{\int }_{0}^{2\pi }|\cos \dfrac {t}{2}|dt=16{\int }_{0}^{\pi }\cos \dfrac {t}{2}dt=32$。
步骤 4:利用极坐标方程进行计算
圆周 ${x}^{2}+{y}^{2}=4x$ 的极坐标方程为 $\rho=4\cos \varphi$,$-\dfrac{\pi}{2}\leq \varphi\leq \dfrac{\pi}{2}$。则 $ds=\sqrt {{\rho}^{2}+{\rho'}^{2}}d\varphi=4d\varphi$,$\sqrt {{x}^{2}+{y}^{2}}ds=4\cos \varphi \cdot 4d\varphi =32\cos \varphi d\varphi =32$。
圆周的方程为 ${x}^{2}+{y}^{2}=4x$,可以改写为 $(x-2)^2 + y^2 = 4$,这是一个以 $(2,0)$ 为圆心,半径为 $2$ 的圆。
步骤 2:利用直角坐标方程进行计算
由方程 ${x}^{2}+{y}^{2}=4x$ 知,$2x+2yy'=4$,得 $y'=\dfrac {2-x}{y}$。于是 $ds=\sqrt {1+{y'}^{2}}dx=\dfrac {2}{\sqrt {{y}^{2}}}dx=\dfrac {2}{\sqrt {4x-{x}^{2}}}dx$。则 ${\int }_{1}\sqrt {{x}^{2}+{y}^{2}}ds=2{\int }_{0}^{4}\sqrt {4x}\dfrac {2}{\sqrt {4x-{x}^{2}}}dx=8{\int }_{0}^{2}\dfrac {dx}{\sqrt {4-x}}=32$。
步骤 3:利用参数方程进行计算
圆周 ${x}^{2}+{y}^{2}=4x$ 的参数方程为 $\left\{\begin{array}{l}x=2+2\cos t\\y=2\sin t\end{array}\right.$,$0\leq t\leq 2\pi$。则 $ds=2dt$,$\sqrt {{x}^{2}+{y}^{2}}ds=2{\int }_{0}^{2\pi }\sqrt {8(1+\cos t)}dt=8{\int }_{0}^{2\pi }|\cos \dfrac {t}{2}|dt=16{\int }_{0}^{\pi }\cos \dfrac {t}{2}dt=32$。
步骤 4:利用极坐标方程进行计算
圆周 ${x}^{2}+{y}^{2}=4x$ 的极坐标方程为 $\rho=4\cos \varphi$,$-\dfrac{\pi}{2}\leq \varphi\leq \dfrac{\pi}{2}$。则 $ds=\sqrt {{\rho}^{2}+{\rho'}^{2}}d\varphi=4d\varphi$,$\sqrt {{x}^{2}+{y}^{2}}ds=4\cos \varphi \cdot 4d\varphi =32\cos \varphi d\varphi =32$。