题目

1.求函数(x,y)=4(x-y)-(x)^2-(y)^2-|||-__的极值.

1.求函数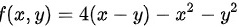 $f(x,y)=4(x-y)-x^2-y^2$ 的极值.

题目解答

答案

(1) 计算偏导数:

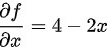
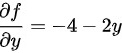
$\dfrac{\partial f}{\partial x}=4-2x$ $\dfrac{\partial f}{\partial y}=-4-2y$

(2) 令偏导数等于0,得到方程组: $\begin{cases} 4-2x=0 \\ -4-2y=0 \end{cases}$

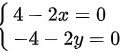
(3) 求解方程组:

x=2,y=-2

(4) 将极值点(2,-2)代入原函数:

$f(2,-2)=4(2-(-2))-4-4=8$

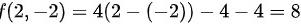
综上,函数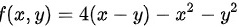 $f(x,y)=4(x-y)-x^2-y^2$ 的极值是8。

解析

步骤 1：计算偏导数
为了找到函数$f(x,y)=4(x-y)-{x}^{2}-{y}^{2}$的极值，我们首先需要计算其关于$x$和$y$的偏导数。
- 对$x$求偏导数：$\dfrac {\partial f}{\partial x}=4-2x$
- 对$y$求偏导数：$\dfrac {\partial f}{\partial y}=-4-2y$

步骤 2：令偏导数等于0
为了找到可能的极值点，我们需要解方程组，其中偏导数等于0。
- $\dfrac {\partial f}{\partial x}=4-2x=0$
- $\dfrac {\partial f}{\partial y}=-4-2y=0$

步骤 3：求解方程组
解上述方程组，得到$x$和$y$的值。
- 从$4-2x=0$得到$x=2$
- 从$-4-2y=0$得到$y=-2$

步骤 4：验证极值点
将$x=2$和$y=-2$代入原函数$f(x,y)$，计算函数值。
- $f(2,-2)=4(2-(-2))-2^2-(-2)^2=4(4)-4-4=16-4-4=8$