题目
求微分方程dfrac (dy)(dx)=3(x)^2y-|||-__的通解.
求微分方程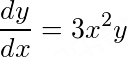 的通解.
的通解.
题目解答
答案
解 当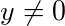 时.将所给方程分离变量,得
时.将所给方程分离变量,得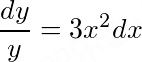 .
.
两端分别积分,有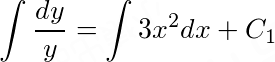 .
.
积分后,得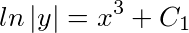 ,
,
从而有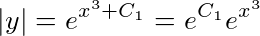 ,即
,即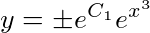 .
.
由于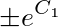 仍是任意常数,把它记作C.于是所给方程的通解为
仍是任意常数,把它记作C.于是所给方程的通解为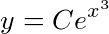 .
.
解析
步骤 1:分离变量
将微分方程$\frac{dy}{dx}=3x^{2}y$分离变量,得到$\frac{dy}{y}=3x^{2}dx$。
步骤 2:积分
对分离变量后的方程两边分别积分,得到$\int \frac{dy}{y}=\int 3x^{2}dx+C_{1}$。
步骤 3:求解
积分后,得到$ln\left |y\right |=x^{3}+C_{1}$,从而有$\left |y\right |=e^{x^{3}+C_{1}}=e^{C_{1}}e^{x^{3}}$,即$y=\pm e^{C_{1}}e^{x^{3}}$。由于$\pm e^{C_{1}}$仍是任意常数,把它记作C。
将微分方程$\frac{dy}{dx}=3x^{2}y$分离变量,得到$\frac{dy}{y}=3x^{2}dx$。
步骤 2:积分
对分离变量后的方程两边分别积分,得到$\int \frac{dy}{y}=\int 3x^{2}dx+C_{1}$。
步骤 3:求解
积分后,得到$ln\left |y\right |=x^{3}+C_{1}$,从而有$\left |y\right |=e^{x^{3}+C_{1}}=e^{C_{1}}e^{x^{3}}$,即$y=\pm e^{C_{1}}e^{x^{3}}$。由于$\pm e^{C_{1}}$仍是任意常数,把它记作C。