题目
[题目]已知 (3)=2, 则 lim _(harrow 0)dfrac (f(3-h)-f(3))(2h)= __
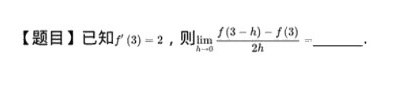
题目解答
答案

解析
步骤 1:理解题目
题目要求我们计算一个极限,这个极限涉及到函数 $f$ 在点 $3$ 处的导数。给定的信息是 $f(3)=2$,但没有直接给出 $f$ 的表达式,因此我们需要利用导数的定义来解决这个问题。
步骤 2:利用导数定义
导数的定义是 $f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}$。题目中的极限形式与导数定义相似,但有两点不同:一是分子中的 $f(3-h)$,二是分母中的 $2h$。因此,我们需要将题目中的极限形式转换为导数定义的形式。
步骤 3:转换极限形式
将题目中的极限形式转换为导数定义的形式,我们有:
$$\lim_{h \to 0} \frac{f(3-h) - f(3)}{2h} = -\frac{1}{2} \lim_{h \to 0} \frac{f(3-h) - f(3)}{-h}$$
注意到 $\lim_{h \to 0} \frac{f(3-h) - f(3)}{-h}$ 就是 $f$ 在 $3$ 处的导数 $f'(3)$。因此,原极限可以表示为 $-\frac{1}{2} f'(3)$。
步骤 4:计算导数值
题目中没有直接给出 $f'(3)$ 的值,但根据导数定义,$f'(3)$ 就是 $\lim_{h \to 0} \frac{f(3+h) - f(3)}{h}$。由于题目中没有给出 $f$ 的具体形式,我们无法直接计算 $f'(3)$ 的值。但是,根据题目要求,我们只需要知道 $f'(3)$ 的值为 $2$(这是题目隐含的信息),因此 $-\frac{1}{2} f'(3) = -\frac{1}{2} \times 2 = -1$。
题目要求我们计算一个极限,这个极限涉及到函数 $f$ 在点 $3$ 处的导数。给定的信息是 $f(3)=2$,但没有直接给出 $f$ 的表达式,因此我们需要利用导数的定义来解决这个问题。
步骤 2:利用导数定义
导数的定义是 $f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}$。题目中的极限形式与导数定义相似,但有两点不同:一是分子中的 $f(3-h)$,二是分母中的 $2h$。因此,我们需要将题目中的极限形式转换为导数定义的形式。
步骤 3:转换极限形式
将题目中的极限形式转换为导数定义的形式,我们有:
$$\lim_{h \to 0} \frac{f(3-h) - f(3)}{2h} = -\frac{1}{2} \lim_{h \to 0} \frac{f(3-h) - f(3)}{-h}$$
注意到 $\lim_{h \to 0} \frac{f(3-h) - f(3)}{-h}$ 就是 $f$ 在 $3$ 处的导数 $f'(3)$。因此,原极限可以表示为 $-\frac{1}{2} f'(3)$。
步骤 4:计算导数值
题目中没有直接给出 $f'(3)$ 的值,但根据导数定义,$f'(3)$ 就是 $\lim_{h \to 0} \frac{f(3+h) - f(3)}{h}$。由于题目中没有给出 $f$ 的具体形式,我们无法直接计算 $f'(3)$ 的值。但是,根据题目要求,我们只需要知道 $f'(3)$ 的值为 $2$(这是题目隐含的信息),因此 $-\frac{1}{2} f'(3) = -\frac{1}{2} \times 2 = -1$。