题目
(4)设 =(e)^-xcos x, 求y"
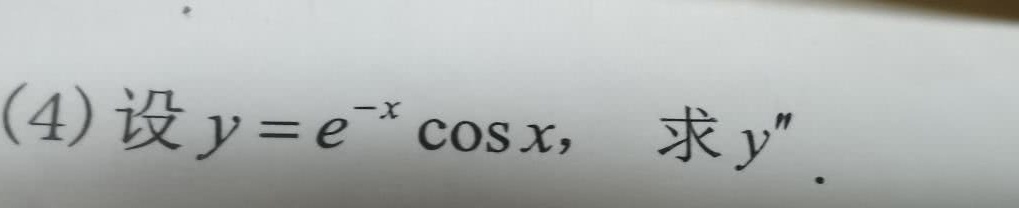
题目解答
答案

解析
步骤 1:求一阶导数
根据乘积法则,$y' = (e^{-x})' \cos x + e^{-x} (\cos x)'$。其中,$(e^{-x})' = -e^{-x}$,$(\cos x)' = -\sin x$。因此,$y' = -e^{-x} \cos x - e^{-x} \sin x$。
步骤 2:求二阶导数
对一阶导数 $y'$ 再次应用乘积法则,$y'' = (-e^{-x} \cos x - e^{-x} \sin x)'$。其中,$(-e^{-x} \cos x)' = e^{-x} \cos x + e^{-x} \sin x$,$(-e^{-x} \sin x)' = e^{-x} \sin x - e^{-x} \cos x$。因此,$y'' = e^{-x} \cos x + e^{-x} \sin x + e^{-x} \sin x - e^{-x} \cos x$。
步骤 3:简化二阶导数
将二阶导数的表达式简化,$y'' = 2e^{-x} \sin x$。
根据乘积法则,$y' = (e^{-x})' \cos x + e^{-x} (\cos x)'$。其中,$(e^{-x})' = -e^{-x}$,$(\cos x)' = -\sin x$。因此,$y' = -e^{-x} \cos x - e^{-x} \sin x$。
步骤 2:求二阶导数
对一阶导数 $y'$ 再次应用乘积法则,$y'' = (-e^{-x} \cos x - e^{-x} \sin x)'$。其中,$(-e^{-x} \cos x)' = e^{-x} \cos x + e^{-x} \sin x$,$(-e^{-x} \sin x)' = e^{-x} \sin x - e^{-x} \cos x$。因此,$y'' = e^{-x} \cos x + e^{-x} \sin x + e^{-x} \sin x - e^{-x} \cos x$。
步骤 3:简化二阶导数
将二阶导数的表达式简化,$y'' = 2e^{-x} \sin x$。