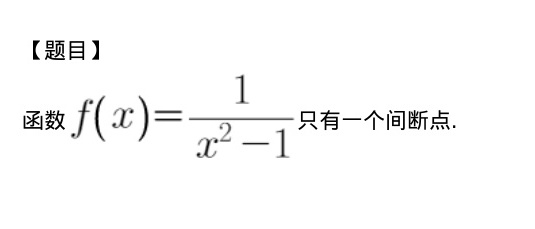
【题目】-|||-函数 (x)=dfrac (1)({x)^2-1} 只有一个间断点.

考查要点：本题主要考查函数间断点的判断，特别是分式函数分母为零时的不连续点。

解题核心思路：

1. 确定分母为零的点：将分母因式分解，解方程找到使分母为零的x值。
2. 判断间断点的存在性：分母为零且函数在该点无定义时，该点即为间断点。
3. 明确间断点数量：根据解的个数确定间断点的数量。

关键点：

• 分式函数的间断点由分母为零的点决定，与分子无关。
• 每个使分母为零的实数解对应一个间断点，需注意解的个数。

函数 $f(x)=\dfrac{1}{x^2-1}$ 的分母为 $x^2-1$，需找到使其为零的x值：

1. 因式分解分母：
   $x^2 - 1 = (x+1)(x-1)$

2. 解方程 $(x+1)(x-1)=0$：
   解得 $x = -1$ 或 $x = 1$。

3. 判断间断点：

   • 当 $x = -1$ 或 $x = 1$ 时，分母为零，函数无定义，因此这两个点均为间断点。
   • 间断点数量为2个，而非题目中所述的“一个”。