题目
设为常数，若反常积分收敛，则的取值范围是（ ） ( A )( B )( C )( D )
设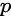
为常数，若反常积分
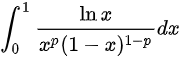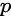收敛，则的取值范围是（ ）
( A )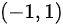
( B )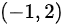
( C )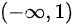
( D )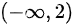
题目解答
答案
当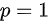
时，反常积分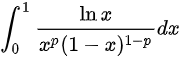
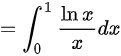，此时级数发散，故排除( B )和( D )。当
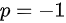时，反常积分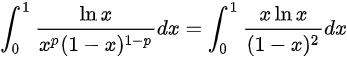
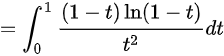。由于
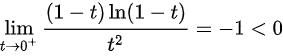
此时级数发散，故排除( C )。则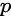的取值范围是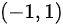。综上所述，答案为( A )。
解析
步骤 1：分析积分的收敛性
反常积分${\int }_{0}^{1}\dfrac {\ln x}{{x}^{p}{(1-x)}^{1-\varphi }}dx$在x=0和x=1处可能发散。因此，需要分别分析这两个点的收敛性。
步骤 2：分析x=0处的收敛性
当x接近0时，${x}^{p}$的收敛性取决于p的值。若p>1，则${x}^{p}$在x=0处发散，若p<1，则${x}^{p}$在x=0处收敛。由于lnx在x=0处发散，因此需要p<1以保证整个积分在x=0处收敛。
步骤 3：分析x=1处的收敛性
当x接近1时，${(1-x)}^{1-\varphi}$的收敛性取决于$\varphi$的值。若$\varphi>1$，则${(1-x)}^{1-\varphi}$在x=1处发散，若$\varphi<1$，则${(1-x)}^{1-\varphi}$在x=1处收敛。由于lnx在x=1处收敛，因此需要$\varphi<1$以保证整个积分在x=1处收敛。
步骤 4：综合分析
根据步骤2和步骤3，p<1且$\varphi<1$。因此，p和$\varphi$的取值范围是(-1,1)。
反常积分${\int }_{0}^{1}\dfrac {\ln x}{{x}^{p}{(1-x)}^{1-\varphi }}dx$在x=0和x=1处可能发散。因此，需要分别分析这两个点的收敛性。
步骤 2：分析x=0处的收敛性
当x接近0时，${x}^{p}$的收敛性取决于p的值。若p>1，则${x}^{p}$在x=0处发散，若p<1，则${x}^{p}$在x=0处收敛。由于lnx在x=0处发散，因此需要p<1以保证整个积分在x=0处收敛。
步骤 3：分析x=1处的收敛性
当x接近1时，${(1-x)}^{1-\varphi}$的收敛性取决于$\varphi$的值。若$\varphi>1$，则${(1-x)}^{1-\varphi}$在x=1处发散，若$\varphi<1$，则${(1-x)}^{1-\varphi}$在x=1处收敛。由于lnx在x=1处收敛，因此需要$\varphi<1$以保证整个积分在x=1处收敛。
步骤 4：综合分析
根据步骤2和步骤3，p<1且$\varphi<1$。因此，p和$\varphi$的取值范围是(-1,1)。