题目
函数 =ln x 在其定义域内是凸的A.对B.错
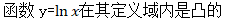
A.对
B.错
题目解答
答案
B. 错
解析
步骤 1:定义域
函数 $y=\ln x$ 的定义域为 $(0,+\infty)$,即所有正实数。
步骤 2:二阶导数
计算函数 $y=\ln x$ 的二阶导数。首先,计算一阶导数 $y'=\frac{1}{x}$。然后,计算二阶导数 $y''=-\frac{1}{x^2}$。
步骤 3:判断凸性
根据二阶导数的符号来判断函数的凸性。如果二阶导数 $y''$ 在定义域内始终小于零,则函数在定义域内是凸的。由于 $y''=-\frac{1}{x^2}$ 在 $(0,+\infty)$ 内始终小于零,因此函数 $y=\ln x$ 在其定义域内是凸的。
函数 $y=\ln x$ 的定义域为 $(0,+\infty)$,即所有正实数。
步骤 2:二阶导数
计算函数 $y=\ln x$ 的二阶导数。首先,计算一阶导数 $y'=\frac{1}{x}$。然后,计算二阶导数 $y''=-\frac{1}{x^2}$。
步骤 3:判断凸性
根据二阶导数的符号来判断函数的凸性。如果二阶导数 $y''$ 在定义域内始终小于零,则函数在定义域内是凸的。由于 $y''=-\frac{1}{x^2}$ 在 $(0,+\infty)$ 内始终小于零,因此函数 $y=\ln x$ 在其定义域内是凸的。