题目
=dfrac (2x)(sqrt {x-3)}+ln (5-x)的定义域是（）A.=dfrac (2x)(sqrt {x-3)}+ln (5-x)B.=dfrac (2x)(sqrt {x-3)}+ln (5-x)C.=dfrac (2x)(sqrt {x-3)}+ln (5-x)D.=dfrac (2x)(sqrt {x-3)}+ln (5-x)
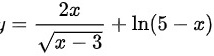的定义域是（）
A.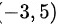
B.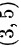
C.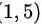
D.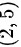
题目解答
答案
解：∵二次根式被开方数大于等于零
∴
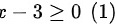
∵分数分母不能为零
∴
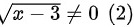
∵对数的真数大于零
∴
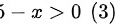
联立(1)(2)(3)式子解得，自变量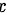
的取值范围是：
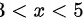，故选B。
解析
步骤 1：确定根号内的条件
由于根号内的表达式$x-3$必须大于等于0，因此有$x-3\geqslant 0$，解得$x\geqslant 3$。
步骤 2：确定分母不为零的条件
由于分母$\sqrt{x-3}$不能为零，因此$x-3\neq 0$，解得$x\neq 3$。
步骤 3：确定对数函数的定义域
由于对数函数$\ln(5-x)$的真数$5-x$必须大于0，因此有$5-x\gt 0$，解得$x\lt 5$。
步骤 4：综合所有条件
综合以上三个条件，得到$x\geqslant 3$，$x\neq 3$，$x\lt 5$，因此$x$的取值范围是$3\lt x\lt 5$。
由于根号内的表达式$x-3$必须大于等于0，因此有$x-3\geqslant 0$，解得$x\geqslant 3$。
步骤 2：确定分母不为零的条件
由于分母$\sqrt{x-3}$不能为零，因此$x-3\neq 0$，解得$x\neq 3$。
步骤 3：确定对数函数的定义域
由于对数函数$\ln(5-x)$的真数$5-x$必须大于0，因此有$5-x\gt 0$，解得$x\lt 5$。
步骤 4：综合所有条件
综合以上三个条件，得到$x\geqslant 3$，$x\neq 3$，$x\lt 5$，因此$x$的取值范围是$3\lt x\lt 5$。