题目
1.求极限 lim _(xarrow 0)dfrac ({e)^x-(e)^sin x}({e)^(x^3)-1}.
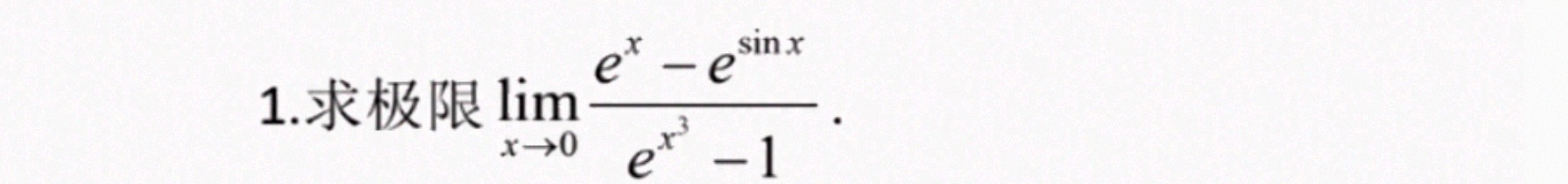
题目解答
答案

解析
步骤 1:使用等价无穷小替换
由于当 $x\rightarrow 0$ 时,$e^x - 1 \sim x$ 和 $e^{\sin x} - 1 \sim \sin x$,因此可以将分子中的 $e^x - e^{\sin x}$ 替换为 $x - \sin x$。
步骤 2:使用等价无穷小替换
由于当 $x\rightarrow 0$ 时,$e^{x^3} - 1 \sim x^3$,因此可以将分母中的 $e^{x^3} - 1$ 替换为 $x^3$。
步骤 3:计算极限
将分子和分母替换为等价无穷小后,原极限变为 $\lim _{x\rightarrow 0}\dfrac {x - \sin x}{x^3}$。由于当 $x\rightarrow 0$ 时,$x - \sin x \sim \dfrac{1}{6}x^3$,因此原极限变为 $\lim _{x\rightarrow 0}\dfrac {\dfrac{1}{6}x^3}{x^3} = \dfrac{1}{6}$。
由于当 $x\rightarrow 0$ 时,$e^x - 1 \sim x$ 和 $e^{\sin x} - 1 \sim \sin x$,因此可以将分子中的 $e^x - e^{\sin x}$ 替换为 $x - \sin x$。
步骤 2:使用等价无穷小替换
由于当 $x\rightarrow 0$ 时,$e^{x^3} - 1 \sim x^3$,因此可以将分母中的 $e^{x^3} - 1$ 替换为 $x^3$。
步骤 3:计算极限
将分子和分母替换为等价无穷小后,原极限变为 $\lim _{x\rightarrow 0}\dfrac {x - \sin x}{x^3}$。由于当 $x\rightarrow 0$ 时,$x - \sin x \sim \dfrac{1}{6}x^3$,因此原极限变为 $\lim _{x\rightarrow 0}\dfrac {\dfrac{1}{6}x^3}{x^3} = \dfrac{1}{6}$。