题目
设函数=f(√x^2+ y^2)，其中=f(√x^2+ y^2)当=f(√x^2+ y^2)时具有二阶连续导数，并且满足=f(√x^2+ y^2)，平面区域=f(√x^2+ y^2)，求二重积分。
设函数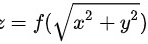
，其中
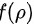当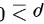
时具有二阶连续导数，并且满足
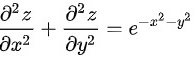，平面区域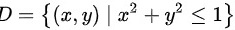
，求二重积分。
题目解答
答案
∵本题所求二重积分为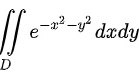
∴
。
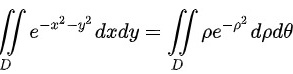∵平面区域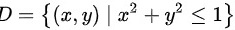
∴
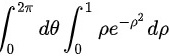
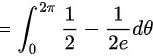
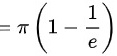
故此，本题的二重积分为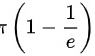
解析
步骤 1：确定二阶偏导数
首先，我们确定函数$z=f(\sqrt {{x}^{2}+{y}^{2}})$的二阶偏导数。设$p=\sqrt {{x}^{2}+{y}^{2}}$，则$z=f(p)$。根据链式法则，我们有：
$$\dfrac {\partial z}{\partial x}=\dfrac {df}{dp}\cdot \dfrac {\partial p}{\partial x}=\dfrac {df}{dp}\cdot \dfrac {x}{\sqrt {{x}^{2}+{y}^{2}}}$$
$$\dfrac {\partial z}{\partial y}=\dfrac {df}{dp}\cdot \dfrac {\partial p}{\partial y}=\dfrac {df}{dp}\cdot \dfrac {y}{\sqrt {{x}^{2}+{y}^{2}}}$$
进一步求二阶偏导数：
$$\dfrac {{\partial }^{2}z}{\partial {x}^{2}}=\dfrac {d^{2}f}{dp^{2}}\cdot \dfrac {{x}^{2}}{{x}^{2}+{y}^{2}}+\dfrac {df}{dp}\cdot \dfrac {{y}^{2}-{x}^{2}}{{({x}^{2}+{y}^{2})}^{3/2}}$$
$$\dfrac {{\partial }^{2}z}{\partial {y}^{2}}=\dfrac {d^{2}f}{dp^{2}}\cdot \dfrac {{y}^{2}}{{x}^{2}+{y}^{2}}+\dfrac {df}{dp}\cdot \dfrac {{x}^{2}-{y}^{2}}{{({x}^{2}+{y}^{2})}^{3/2}}$$
步骤 2：求和并简化
将上述二阶偏导数相加，得到：
$$\dfrac {{\partial }^{2}z}{\partial {x}^{2}}+\dfrac {{\partial }^{2}z}{\partial {y}^{2}}=\dfrac {d^{2}f}{dp^{2}}+\dfrac {df}{dp}\cdot \dfrac {1}{p}$$
根据题目条件，我们有：
$$\dfrac {d^{2}f}{dp^{2}}+\dfrac {df}{dp}\cdot \dfrac {1}{p}={e}^{-{x}^{2}-{y}^{2}}$$
步骤 3：求解二重积分
根据题目条件，我们要求的二重积分为：
$$\iint {e}^{-{x}^{2}-{y}^{2}}dxdy$$
在极坐标系下，$x=r\cos \theta$，$y=r\sin \theta$，$dxdy=rdrd\theta$，则积分变为：
$$\int_{0}^{2\pi }\int_{0}^{1}{e}^{-{r}^{2}}rdrd\theta$$
步骤 4：计算积分
计算上述积分，我们有：
$$\int_{0}^{2\pi }\int_{0}^{1}{e}^{-{r}^{2}}rdrd\theta =\int_{0}^{2\pi }\left[-\dfrac {1}{2}{e}^{-{r}^{2}}\right]_{0}^{1}d\theta =\int_{0}^{2\pi }\left(-\dfrac {1}{2}{e}^{-1}+\dfrac {1}{2}\right)d\theta =\pi \left(1-\dfrac {1}{e}\right)$$
首先，我们确定函数$z=f(\sqrt {{x}^{2}+{y}^{2}})$的二阶偏导数。设$p=\sqrt {{x}^{2}+{y}^{2}}$，则$z=f(p)$。根据链式法则，我们有：
$$\dfrac {\partial z}{\partial x}=\dfrac {df}{dp}\cdot \dfrac {\partial p}{\partial x}=\dfrac {df}{dp}\cdot \dfrac {x}{\sqrt {{x}^{2}+{y}^{2}}}$$
$$\dfrac {\partial z}{\partial y}=\dfrac {df}{dp}\cdot \dfrac {\partial p}{\partial y}=\dfrac {df}{dp}\cdot \dfrac {y}{\sqrt {{x}^{2}+{y}^{2}}}$$
进一步求二阶偏导数：
$$\dfrac {{\partial }^{2}z}{\partial {x}^{2}}=\dfrac {d^{2}f}{dp^{2}}\cdot \dfrac {{x}^{2}}{{x}^{2}+{y}^{2}}+\dfrac {df}{dp}\cdot \dfrac {{y}^{2}-{x}^{2}}{{({x}^{2}+{y}^{2})}^{3/2}}$$
$$\dfrac {{\partial }^{2}z}{\partial {y}^{2}}=\dfrac {d^{2}f}{dp^{2}}\cdot \dfrac {{y}^{2}}{{x}^{2}+{y}^{2}}+\dfrac {df}{dp}\cdot \dfrac {{x}^{2}-{y}^{2}}{{({x}^{2}+{y}^{2})}^{3/2}}$$
步骤 2：求和并简化
将上述二阶偏导数相加，得到：
$$\dfrac {{\partial }^{2}z}{\partial {x}^{2}}+\dfrac {{\partial }^{2}z}{\partial {y}^{2}}=\dfrac {d^{2}f}{dp^{2}}+\dfrac {df}{dp}\cdot \dfrac {1}{p}$$
根据题目条件，我们有：
$$\dfrac {d^{2}f}{dp^{2}}+\dfrac {df}{dp}\cdot \dfrac {1}{p}={e}^{-{x}^{2}-{y}^{2}}$$
步骤 3：求解二重积分
根据题目条件，我们要求的二重积分为：
$$\iint {e}^{-{x}^{2}-{y}^{2}}dxdy$$
在极坐标系下，$x=r\cos \theta$，$y=r\sin \theta$，$dxdy=rdrd\theta$，则积分变为：
$$\int_{0}^{2\pi }\int_{0}^{1}{e}^{-{r}^{2}}rdrd\theta$$
步骤 4：计算积分
计算上述积分，我们有：
$$\int_{0}^{2\pi }\int_{0}^{1}{e}^{-{r}^{2}}rdrd\theta =\int_{0}^{2\pi }\left[-\dfrac {1}{2}{e}^{-{r}^{2}}\right]_{0}^{1}d\theta =\int_{0}^{2\pi }\left(-\dfrac {1}{2}{e}^{-1}+\dfrac {1}{2}\right)d\theta =\pi \left(1-\dfrac {1}{e}\right)$$