题目
计算= zdxdydz , = zdxdydz是由圆锥面= zdxdydz与旋转抛物面= zdxdydz所围成的立体。
计算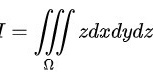
, 
是由圆锥面
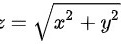与旋转抛物面
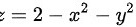所围成的立体。
题目解答
答案
由于是由圆锥面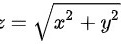与旋转抛物面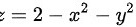所围成的立体。则积分区域的投影区域为
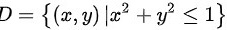。将三重积分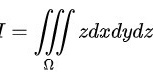化为柱面坐标下的积分可得：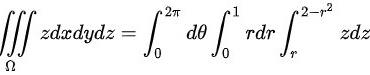
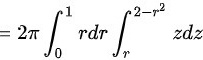
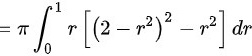
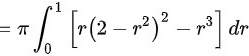
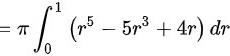
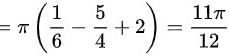
则三重积分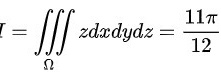
。
解析
步骤 1：确定积分区域
由于是由圆锥面$z=\sqrt {{x}^{2}+{y}^{2}}$与旋转抛物面$z=2-{x}^{2}-{y}^{2}$所围成的立体。则积分区域的投影区域为$D=\{ (x,y)|{x}^{2}+{y}^{2}\leqslant 1\} $。
步骤 2：将三重积分化为柱面坐标下的积分
将三重积分= zdxdydz Ω化为柱面坐标下的积分可得：Ω ${\iint }_{U}=dxdydx={\int }_{0}^{2\pi }d\theta {\int }_{0}^{1}rdr{\int }_{5}^{2-{r}^{2}}^{2-{r}^{2}}2dx$1 2-r^2 $=2\pi $ rdr zdz
步骤 3：计算积分
$=\pi {\int }_{0}^{1}r[ {(2-{r}^{2})}^{2}-{r}^{2}] dr$
$=\pi {\int }_{0}^{1}[ r{(2-{r}^{2})}^{2}-{r}^{3}] dr$
$=\pi {\int }_{0}^{1}({r}^{5}-5{r}^{3}+4r)dr$
$=\pi (\dfrac {1}{6}-\dfrac {5}{4}+2)=\dfrac {11\pi }{12}$
由于是由圆锥面$z=\sqrt {{x}^{2}+{y}^{2}}$与旋转抛物面$z=2-{x}^{2}-{y}^{2}$所围成的立体。则积分区域的投影区域为$D=\{ (x,y)|{x}^{2}+{y}^{2}\leqslant 1\} $。
步骤 2：将三重积分化为柱面坐标下的积分
将三重积分= zdxdydz Ω化为柱面坐标下的积分可得：Ω ${\iint }_{U}=dxdydx={\int }_{0}^{2\pi }d\theta {\int }_{0}^{1}rdr{\int }_{5}^{2-{r}^{2}}^{2-{r}^{2}}2dx$1 2-r^2 $=2\pi $ rdr zdz
步骤 3：计算积分
$=\pi {\int }_{0}^{1}r[ {(2-{r}^{2})}^{2}-{r}^{2}] dr$
$=\pi {\int }_{0}^{1}[ r{(2-{r}^{2})}^{2}-{r}^{3}] dr$
$=\pi {\int }_{0}^{1}({r}^{5}-5{r}^{3}+4r)dr$
$=\pi (\dfrac {1}{6}-\dfrac {5}{4}+2)=\dfrac {11\pi }{12}$