题目
6.设 ^3-2xz+y=0, 求 a^2z/ax^2, dfrac ({a)^2z}(partial {y)^2}.
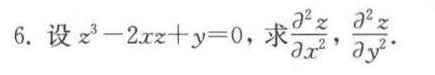
题目解答
答案

解析
步骤 1:求 $\dfrac {\partial z}{\partial x}$ 和 $\dfrac {\partial z}{\partial y}$
令 $F(x,y,z)={z}^{3}-2xz+y$ ,由隐函数存在定理,得 $\dfrac {\partial z}{\partial x}=-\dfrac {{F}_{x}}{{F}_{z}}=-\dfrac {-2z}{3{z}^{2}-2x}=\dfrac {2z}{3{z}^{2}-2x}$ (当 $3{z}^{2}-2x\neq 0$ 时). $\dfrac {\partial z}{\partial y}=-\dfrac {F'}{{F}_{z}}=-\dfrac {1}{3{z}^{2}-2x}$ (当 $3{x}^{2}-2x\neq 0$ 时).
步骤 2:求 $\dfrac {{\partial }^{2}z}{\partial {x}^{2}}$
对 $\dfrac {\partial z}{\partial x}$ 关于x求偏导,得 $\dfrac {{\partial }^{2}z}{\partial {x}^{2}}=\dfrac {-(6{x}^{2}+4x)\dfrac {2z}{3{z}^{2}-2x}+4z}{{(3{z}^{2}-2x)}^{2}}=\dfrac {-(6{x}^{2}+4x)\cdot 2z+4z(3{z}^{2}-2x)}{{(3{z}^{2}-2x)}^{3}}=\dfrac {16xz}{{(3{z}^{2}-2x)}^{3}}$ (当 $3{z}^{2}-2x\neq 0$ 时).
步骤 3:求 $\dfrac {{\partial }^{2}z}{\partial {y}^{2}}$
对 $\dfrac {\partial z}{\partial y}$ 关于y再求偏导,得 $\dfrac {{\partial }^{2}z}{\partial {y}^{2}}=\dfrac {6z\dfrac {\partial z}{\partial y}}{{(3{z}^{2}-2x)}^{2}}=-\dfrac {6z}{{(3{z}^{2}-2x)}^{3}}$ (当 $3{z}^{2}-2x\neq 0$ 时).
令 $F(x,y,z)={z}^{3}-2xz+y$ ,由隐函数存在定理,得 $\dfrac {\partial z}{\partial x}=-\dfrac {{F}_{x}}{{F}_{z}}=-\dfrac {-2z}{3{z}^{2}-2x}=\dfrac {2z}{3{z}^{2}-2x}$ (当 $3{z}^{2}-2x\neq 0$ 时). $\dfrac {\partial z}{\partial y}=-\dfrac {F'}{{F}_{z}}=-\dfrac {1}{3{z}^{2}-2x}$ (当 $3{x}^{2}-2x\neq 0$ 时).
步骤 2:求 $\dfrac {{\partial }^{2}z}{\partial {x}^{2}}$
对 $\dfrac {\partial z}{\partial x}$ 关于x求偏导,得 $\dfrac {{\partial }^{2}z}{\partial {x}^{2}}=\dfrac {-(6{x}^{2}+4x)\dfrac {2z}{3{z}^{2}-2x}+4z}{{(3{z}^{2}-2x)}^{2}}=\dfrac {-(6{x}^{2}+4x)\cdot 2z+4z(3{z}^{2}-2x)}{{(3{z}^{2}-2x)}^{3}}=\dfrac {16xz}{{(3{z}^{2}-2x)}^{3}}$ (当 $3{z}^{2}-2x\neq 0$ 时).
步骤 3:求 $\dfrac {{\partial }^{2}z}{\partial {y}^{2}}$
对 $\dfrac {\partial z}{\partial y}$ 关于y再求偏导,得 $\dfrac {{\partial }^{2}z}{\partial {y}^{2}}=\dfrac {6z\dfrac {\partial z}{\partial y}}{{(3{z}^{2}-2x)}^{2}}=-\dfrac {6z}{{(3{z}^{2}-2x)}^{3}}$ (当 $3{z}^{2}-2x\neq 0$ 时).