题目
袋子中有5个不同的小球,一次任选 2 个, 有 ( )种 选法。
袋子中有5个不同的小球,一次任选 2 个, 有 ( )种 选法。
题目解答
答案
∵从5个不同的小球,一次任选 2 个
根据组合的定义:般地,从n个不同的元素中,任取m(m≤n)个元素为一组,叫作从n个不同元素中任取m个元素的一个组合
以及组合的计算公式: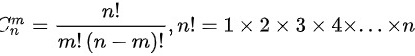
∴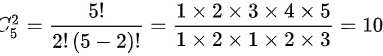
解析
步骤 1:确定问题类型
问题要求从5个不同的小球中任选2个,属于组合问题,因为选法不考虑顺序。
步骤 2:应用组合公式
组合公式为 ${C}_{n}^{m}=\dfrac {n!}{m!(n-m)!}$,其中 $n$ 是总数,$m$ 是选取的数量。
步骤 3:计算组合数
将 $n=5$ 和 $m=2$ 代入组合公式,计算 ${C}_{5}^{2}$ 的值。
问题要求从5个不同的小球中任选2个,属于组合问题,因为选法不考虑顺序。
步骤 2:应用组合公式
组合公式为 ${C}_{n}^{m}=\dfrac {n!}{m!(n-m)!}$,其中 $n$ 是总数,$m$ 是选取的数量。
步骤 3:计算组合数
将 $n=5$ 和 $m=2$ 代入组合公式,计算 ${C}_{5}^{2}$ 的值。