题目
yt B-|||-C A-|||-0如图，抛物线y=ax2+c经过正方形OABC的三个顶点A，B，C，点B在y轴上，则ac的值为（ ）A. -1B. -2C. -3D. -4
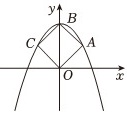如图，抛物线y=ax2+c经过正方形OABC的三个顶点A，B，C，点B在y轴上，则ac的值为（ ）- A. -1
- B. -2
- C. -3
- D. -4
题目解答
答案
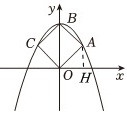解：过A作AH⊥x轴于H，∵四边形ABCO是正方形，
∴∠AOB=45°，
∴∠AOH=45°，
∴AH=OH，
设A（m,m），则B（0，2m），
∴$\left\{\begin{array}{l}{m=a{m}^{2}+c}\\{2m=c}\end{array}\right.$，
解得am=-1，m=$\frac{c}{2}$，
∴ac的值为-2，
故选：B．
解析
步骤 1：确定正方形的顶点坐标
由于正方形OABC的顶点O在原点，B在y轴上，且正方形的边长为m，所以A点的坐标为(m, m)，B点的坐标为(0, 2m)，C点的坐标为(m, 0)。
步骤 2：将顶点坐标代入抛物线方程
将A点坐标(m, m)代入抛物线方程y=ax^{2}+c，得到m=am^{2}+c。
将B点坐标(0, 2m)代入抛物线方程y=ax^{2}+c，得到2m=c。
步骤 3：解方程组求解ac的值
由步骤2得到的方程组$\left\{\begin{array}{l}{m=a{m}^{2}+c}\\{2m=c}\end{array}\right.$，将c=2m代入第一个方程，得到m=am^{2}+2m，化简得到am^{2}+m=0，即am=-1。由于m=$\frac{c}{2}$，所以ac的值为-2。
由于正方形OABC的顶点O在原点，B在y轴上，且正方形的边长为m，所以A点的坐标为(m, m)，B点的坐标为(0, 2m)，C点的坐标为(m, 0)。
步骤 2：将顶点坐标代入抛物线方程
将A点坐标(m, m)代入抛物线方程y=ax^{2}+c，得到m=am^{2}+c。
将B点坐标(0, 2m)代入抛物线方程y=ax^{2}+c，得到2m=c。
步骤 3：解方程组求解ac的值
由步骤2得到的方程组$\left\{\begin{array}{l}{m=a{m}^{2}+c}\\{2m=c}\end{array}\right.$，将c=2m代入第一个方程，得到m=am^{2}+2m，化简得到am^{2}+m=0，即am=-1。由于m=$\frac{c}{2}$，所以ac的值为-2。