题目
点(1,3,0)到平面x+2y+2z-10=0的距离为_____
点(1,3,0)到平面x+2y+2z-10=0的距离为_____
题目解答
答案
解:由点到平面距离公式得
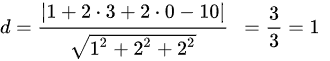
故点(1,3,0)到平面x+2y+2z-10=0的距离为1
解析
考查要点:本题主要考查点到平面的距离公式的应用,需要掌握平面方程的一般形式及公式中各参数的对应关系。
解题核心思路:
- 识别平面方程:将题目中的平面方程整理为标准形式$Ax + By + Cz + D = 0$,确定系数$A, B, C$和常数项$D$。
- 代入公式计算:直接套用点到平面的距离公式$d = \dfrac{|Ax_0 + By_0 + Cz_0 + D|}{\sqrt{A^2 + B^2 + C^2}}$,注意符号的正确代入。
破题关键点:
- 正确提取平面方程的系数,尤其是常数项$D$的符号。
- 准确代入点的坐标,避免计算错误。
步骤1:整理平面方程
题目给出的平面方程为$x + 2y + 2z - 10 = 0$,可改写为标准形式:
$1 \cdot x + 2 \cdot y + 2 \cdot z + (-10) = 0$
对应系数为$A = 1$,$B = 2$,$C = 2$,常数项$D = -10$。
步骤2:代入点到平面的距离公式
点$(1, 3, 0)$的坐标代入公式:
$d = \dfrac{|A \cdot x_0 + B \cdot y_0 + C \cdot z_0 + D|}{\sqrt{A^2 + B^2 + C^2}}$
计算分子部分:
$1 \cdot 1 + 2 \cdot 3 + 2 \cdot 0 + (-10) = 1 + 6 + 0 - 10 = -3$
取绝对值得到分子为$3$。
步骤3:计算分母
分母为$\sqrt{1^2 + 2^2 + 2^2} = \sqrt{1 + 4 + 4} = \sqrt{9} = 3$。
步骤4:求距离
最终距离为:
$d = \dfrac{3}{3} = 1$