题目
求dfrac (d)(dx)[ (int )_(2)^eln xdx] =________.
求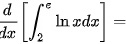 ________.
________.
题目解答
答案
因为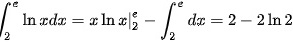
所以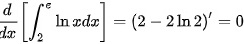
故答案为:
解析
步骤 1:理解问题
题目要求我们求解 $\dfrac {d}{dx} \int \ln x \, dx$。首先,我们需要计算不定积分 $\int \ln x \, dx$,然后对结果求导。
步骤 2:计算不定积分
使用分部积分法计算 $\int \ln x \, dx$。设 $u = \ln x$,$dv = dx$,则 $du = \dfrac{1}{x} dx$,$v = x$。根据分部积分公式 $\int u \, dv = uv - \int v \, du$,我们有:
$$
\int \ln x \, dx = x \ln x - \int x \cdot \dfrac{1}{x} \, dx = x \ln x - \int 1 \, dx = x \ln x - x + C
$$
其中 $C$ 是积分常数。
步骤 3:求导
现在我们对不定积分的结果求导,即求 $\dfrac {d}{dx} (x \ln x - x + C)$。根据导数的线性性质,我们有:
$$
\dfrac {d}{dx} (x \ln x - x + C) = \dfrac {d}{dx} (x \ln x) - \dfrac {d}{dx} (x) + \dfrac {d}{dx} (C)
$$
其中 $\dfrac {d}{dx} (x \ln x)$ 可以使用乘积法则计算,$\dfrac {d}{dx} (x) = 1$,$\dfrac {d}{dx} (C) = 0$。因此:
$$
\dfrac {d}{dx} (x \ln x) = \ln x + x \cdot \dfrac{1}{x} = \ln x + 1
$$
所以:
$$
\dfrac {d}{dx} (x \ln x - x + C) = \ln x + 1 - 1 + 0 = \ln x
$$
题目要求我们求解 $\dfrac {d}{dx} \int \ln x \, dx$。首先,我们需要计算不定积分 $\int \ln x \, dx$,然后对结果求导。
步骤 2:计算不定积分
使用分部积分法计算 $\int \ln x \, dx$。设 $u = \ln x$,$dv = dx$,则 $du = \dfrac{1}{x} dx$,$v = x$。根据分部积分公式 $\int u \, dv = uv - \int v \, du$,我们有:
$$
\int \ln x \, dx = x \ln x - \int x \cdot \dfrac{1}{x} \, dx = x \ln x - \int 1 \, dx = x \ln x - x + C
$$
其中 $C$ 是积分常数。
步骤 3:求导
现在我们对不定积分的结果求导,即求 $\dfrac {d}{dx} (x \ln x - x + C)$。根据导数的线性性质,我们有:
$$
\dfrac {d}{dx} (x \ln x - x + C) = \dfrac {d}{dx} (x \ln x) - \dfrac {d}{dx} (x) + \dfrac {d}{dx} (C)
$$
其中 $\dfrac {d}{dx} (x \ln x)$ 可以使用乘积法则计算,$\dfrac {d}{dx} (x) = 1$,$\dfrac {d}{dx} (C) = 0$。因此:
$$
\dfrac {d}{dx} (x \ln x) = \ln x + x \cdot \dfrac{1}{x} = \ln x + 1
$$
所以:
$$
\dfrac {d}{dx} (x \ln x - x + C) = \ln x + 1 - 1 + 0 = \ln x
$$