题目
求极限lim _(xarrow 0)((dfrac {sin x)(x))}^dfrac (1{ln (1+{x)^2)}}
求极限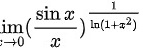
题目解答
答案
依题意,计算
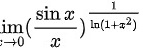
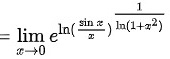
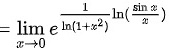
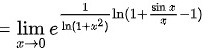
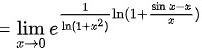
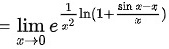
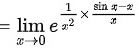
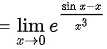
对该极限使用洛必达法则,将极限的分子分母同时求导,得
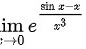
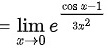
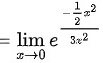
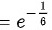
解析
步骤 1:将原极限表达式转换为指数形式
原极限表达式为$\lim _{x\rightarrow 0}{(\dfrac {\sin x}{x})}^{\dfrac {1}{\ln (1+{x}^{2})}}$,可以转换为$e$的指数形式,即$\lim _{x\rightarrow 0}{e}^{\ln (\dfrac {\sin x}{x})\dfrac {1}{\ln (1+{x}^{2})}}$。
步骤 2:将$\dfrac {\sin x}{x}$替换为$1+\dfrac {\sin x-x}{x}$
由于$\lim _{x\rightarrow 0}\dfrac {\sin x}{x}=1$,所以可以将$\dfrac {\sin x}{x}$替换为$1+\dfrac {\sin x-x}{x}$,从而得到$\lim _{x\rightarrow 0}{e}^{\dfrac {1}{\ln (1+{x}^{2})}\ln (1+\dfrac {\sin x-x}{x})}$。
步骤 3:将$\ln (1+\dfrac {\sin x-x}{x})$替换为$\dfrac {\sin x-x}{x}$
由于$\lim _{x\rightarrow 0}\dfrac {\sin x-x}{x}=0$,所以可以将$\ln (1+\dfrac {\sin x-x}{x})$替换为$\dfrac {\sin x-x}{x}$,从而得到$\lim _{x\rightarrow 0}{e}^{\dfrac {1}{{x}^{2}}\times \dfrac {\sin x-x}{x}}$。
步骤 4:使用洛必达法则求解极限
对$\lim _{x\rightarrow 0}\dfrac {\sin x-x}{x^3}$使用洛必达法则,将极限的分子分母同时求导,得$\lim _{x\rightarrow 0}\dfrac {\cos x-1}{3x^2}$,再次使用洛必达法则,得$\lim _{x\rightarrow 0}\dfrac {-\sin x}{6x}$,再次使用洛必达法则,得$\lim _{x\rightarrow 0}\dfrac {-\cos x}{6}=-\dfrac {1}{6}$。
步骤 5:将求得的极限值代入原式
将$\lim _{x\rightarrow 0}\dfrac {\sin x-x}{x^3}=-\dfrac {1}{6}$代入原式,得$\lim _{x\rightarrow 0}{e}^{\dfrac {1}{{x}^{2}}\times \dfrac {\sin x-x}{x}}=\lim _{x\rightarrow 0}{e}^{\dfrac {-\dfrac {1}{2}{x}^{2}}{3{x}^{2}}}={e}^{-\dfrac {1}{6}}$。
原极限表达式为$\lim _{x\rightarrow 0}{(\dfrac {\sin x}{x})}^{\dfrac {1}{\ln (1+{x}^{2})}}$,可以转换为$e$的指数形式,即$\lim _{x\rightarrow 0}{e}^{\ln (\dfrac {\sin x}{x})\dfrac {1}{\ln (1+{x}^{2})}}$。
步骤 2:将$\dfrac {\sin x}{x}$替换为$1+\dfrac {\sin x-x}{x}$
由于$\lim _{x\rightarrow 0}\dfrac {\sin x}{x}=1$,所以可以将$\dfrac {\sin x}{x}$替换为$1+\dfrac {\sin x-x}{x}$,从而得到$\lim _{x\rightarrow 0}{e}^{\dfrac {1}{\ln (1+{x}^{2})}\ln (1+\dfrac {\sin x-x}{x})}$。
步骤 3:将$\ln (1+\dfrac {\sin x-x}{x})$替换为$\dfrac {\sin x-x}{x}$
由于$\lim _{x\rightarrow 0}\dfrac {\sin x-x}{x}=0$,所以可以将$\ln (1+\dfrac {\sin x-x}{x})$替换为$\dfrac {\sin x-x}{x}$,从而得到$\lim _{x\rightarrow 0}{e}^{\dfrac {1}{{x}^{2}}\times \dfrac {\sin x-x}{x}}$。
步骤 4:使用洛必达法则求解极限
对$\lim _{x\rightarrow 0}\dfrac {\sin x-x}{x^3}$使用洛必达法则,将极限的分子分母同时求导,得$\lim _{x\rightarrow 0}\dfrac {\cos x-1}{3x^2}$,再次使用洛必达法则,得$\lim _{x\rightarrow 0}\dfrac {-\sin x}{6x}$,再次使用洛必达法则,得$\lim _{x\rightarrow 0}\dfrac {-\cos x}{6}=-\dfrac {1}{6}$。
步骤 5:将求得的极限值代入原式
将$\lim _{x\rightarrow 0}\dfrac {\sin x-x}{x^3}=-\dfrac {1}{6}$代入原式,得$\lim _{x\rightarrow 0}{e}^{\dfrac {1}{{x}^{2}}\times \dfrac {\sin x-x}{x}}=\lim _{x\rightarrow 0}{e}^{\dfrac {-\dfrac {1}{2}{x}^{2}}{3{x}^{2}}}={e}^{-\dfrac {1}{6}}$。