题目
已知2x是函数2x的一个原函数,则下列各式正确的是( ) 2x.2x2x.2x,2x.2x,2x.2x,
已知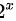 是函数
是函数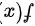 的一个原函数,则下列各式正确的是( )
的一个原函数,则下列各式正确的是( )
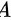 .
.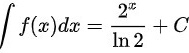
 .
.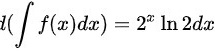 ,
,
 .
.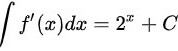 ,
,
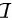 .
.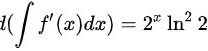 ,
,
题目解答
答案
已知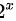 是函数
是函数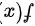 的一个原函数,
的一个原函数,
∴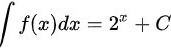 ,故
,故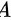 错误;
错误;
∴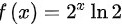 ,
,
∴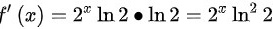 ,
,
∴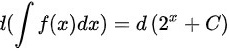
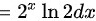 ,
,
故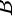 正确;
正确;
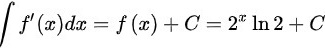 ,
,
故 错误;
错误;
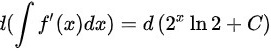 ,
,
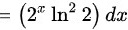 ,
,
故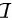 错误。
错误。
故选: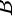 。
。
解析
步骤 1:分析选项A
根据上述分析,$\int f(x)dx = \frac{2^x}{\ln 2} + C$,因此选项A正确。
步骤 2:分析选项B
由于$f(x) = 2^x$,则$f'(x) = 2^x \ln 2$。因此,$\iint f(x)dx = d(\int f(x)dx) = d(\frac{2^x}{\ln 2} + C) = 2^x \ln 2 dx$,故选项B正确。
步骤 3:分析选项C
由于$f'(x) = 2^x \ln 2$,则$\int f'(x)dx = \int 2^x \ln 2 dx = 2^x + C$,故选项C错误。
步骤 4:分析选项D
由于$f'(x) = 2^x \ln 2$,则$\iint f'(x)dx = d(\int f'(x)dx) = d(2^x + C) = 2^x \ln 2 dx$,故选项D错误。
根据上述分析,$\int f(x)dx = \frac{2^x}{\ln 2} + C$,因此选项A正确。
步骤 2:分析选项B
由于$f(x) = 2^x$,则$f'(x) = 2^x \ln 2$。因此,$\iint f(x)dx = d(\int f(x)dx) = d(\frac{2^x}{\ln 2} + C) = 2^x \ln 2 dx$,故选项B正确。
步骤 3:分析选项C
由于$f'(x) = 2^x \ln 2$,则$\int f'(x)dx = \int 2^x \ln 2 dx = 2^x + C$,故选项C错误。
步骤 4:分析选项D
由于$f'(x) = 2^x \ln 2$,则$\iint f'(x)dx = d(\int f'(x)dx) = d(2^x + C) = 2^x \ln 2 dx$,故选项D错误。