设函数 y=f(x) 在点x0取得极小值,则不正确的是设函数 y=f(x) 在点x0取得极小值,则不正确的是

题目解答
答案
设函数 y = f(x) 在点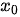 取得极小值,根据极值的定义和性质,我们可以分析每个选项:
取得极小值,根据极值的定义和性质,我们可以分析每个选项:
A. 点 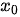 是驻点
是驻点
驻点是指函数的导数为零的点。对于极小值点,其导数为零是必要条件,因此这个说法是正确的。
B. 点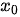 是拐点
是拐点
拐点是指函数图形凹凸性发生变化的点,即二阶导数变号的点。极小值点不一定是拐点。例如,考虑函数 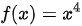 ,其在 x = 0 处取得极小值,但 x = 0不是拐点。因此,这个说法是不正确的。
,其在 x = 0 处取得极小值,但 x = 0不是拐点。因此,这个说法是不正确的。
C. 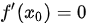
如前所述,极小值点处的导数为零,因此这个说法是正确的。
D. 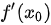 不存在
不存在
如果函数在极小值点的导数不存在,则该点不能是极值点。因此,这个说法也是正确的。
综上所述,不正确的选项是 B。
解析
考查要点:本题主要考查极值点的性质,包括驻点、拐点的定义,以及导数在极值点处的条件。
解题核心思路:
- 极值的必要条件:若函数在某点可导且取得极值,则该点必为驻点(导数为零)。
- 拐点的定义:拐点是函数凹凸性发生改变的点,与极值点无必然联系。
- 导数不存在的情况:若极值点处导数不存在,则该点不是驻点,但仍是极值点。
破题关键点:
- 选项B:极小值点不一定是拐点,需通过反例(如$f(x)=x^4$在$x=0$处)说明。
- 选项A和C:若导数存在,则极小值点必为驻点且导数为零;若导数不存在,则选项A和C均不成立,但题目未限定导数存在性,需结合选项判断。
选项分析:
-
选项A:点$x_0$是驻点
驻点要求$f'(x_0)=0$。若$f(x)$在$x_0$处可导且取得极小值,则$f'(x_0)=0$,此时$x_0$是驻点。但若导数不存在,则$x_0$不是驻点。因此,选项A的正确性依赖于导数是否存在。 -
选项B:点$x_0$是拐点
拐点要求函数凹凸性改变,即二阶导数变号。极小值点仅要求一阶导数为零或不存在,与凹凸性无关。例如,$f(x)=x^4$在$x=0$处取得极小值,但此处二阶导数为$0$且周围凹凸性不变,故$x=0$不是拐点。因此,选项B不成立。 -
选项C:$f'(x_0)=0$
若$f(x)$在$x_0$处可导且取得极小值,则$f'(x_0)=0$。但若导数不存在,则$f'(x_0)$无意义。因此,选项C的正确性同样依赖于导数是否存在。 -
选项D:$f'(x_0)$不存在
若$f(x)$在$x_0$处不可导,则$x_0$仍可能是极小值点(如$f(x)=|x|$在$x=0$处)。因此,选项D可能成立。
结论:选项B的描述与极值点的性质矛盾,因此不正确。