题目
设X,Y的概率密度为-|||-f(x,y)= ) 1,|y|leqslant x,0leqslant xleqslant 1 0, .-|||-(1)求关于X,Y的边缘概率密度;-|||-(2)求E(X),E(Y )及D(X),D(Y);-|||-(3)求cov(X,Y).
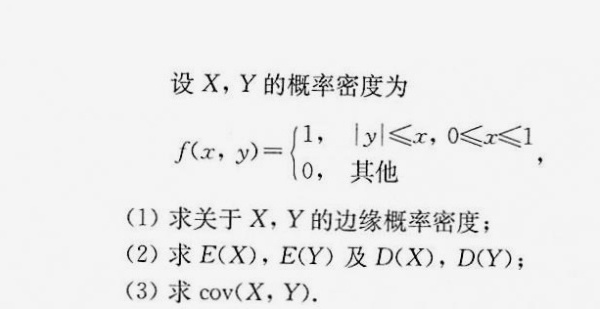
题目解答
答案

解析
步骤 1:求关于X的边缘概率密度
根据边缘概率密度的定义,我们有 ${f}_{x}(x)={\int }_{-\infty }^{\infty }f(x,y)dy$。由于f(x,y)在$|y|\leqslant x,0\leqslant x\leqslant 1$时为1,其他情况为0,因此我们只需在$-x\leqslant y\leqslant x$的范围内积分。
步骤 2:求关于Y的边缘概率密度
根据边缘概率密度的定义,我们有 ${f}_{y}(y)={\int }_{-\infty }^{\infty }f(x,y)dx$。由于f(x,y)在$|y|\leqslant x,0\leqslant x\leqslant 1$时为1,其他情况为0,因此我们只需在$|y|\leqslant x\leqslant 1$的范围内积分。
步骤 3:求E(X)和E(Y)
根据期望的定义,我们有 $E(X)={\int }_{-\infty }^{\infty }x{f}_{x}(x)dx$ 和 $E(Y)={\int }_{-\infty }^{\infty }y{f}_{y}(y)dy$。
步骤 4:求D(X)和D(Y)
根据方差的定义,我们有 $D(X)=E({X}^{2})-{[E(X)]}^{2}$ 和 $D(Y)=E({Y}^{2})-{[E(Y)]}^{2}$,其中 $E({X}^{2})={\int }_{-\infty }^{\infty }{x}^{2}{f}_{x}(x)dx$ 和 $E({Y}^{2})={\int }_{-\infty }^{\infty }{y}^{2}{f}_{y}(y)dy$。
步骤 5:求cov(X,Y)
根据协方差的定义,我们有 $cov(X,Y)=E(XY)-E(X)E(Y)$,其中 $E(XY)={\iint }_{-\infty }^{\infty }xyf(x,y)dxdy$。
根据边缘概率密度的定义,我们有 ${f}_{x}(x)={\int }_{-\infty }^{\infty }f(x,y)dy$。由于f(x,y)在$|y|\leqslant x,0\leqslant x\leqslant 1$时为1,其他情况为0,因此我们只需在$-x\leqslant y\leqslant x$的范围内积分。
步骤 2:求关于Y的边缘概率密度
根据边缘概率密度的定义,我们有 ${f}_{y}(y)={\int }_{-\infty }^{\infty }f(x,y)dx$。由于f(x,y)在$|y|\leqslant x,0\leqslant x\leqslant 1$时为1,其他情况为0,因此我们只需在$|y|\leqslant x\leqslant 1$的范围内积分。
步骤 3:求E(X)和E(Y)
根据期望的定义,我们有 $E(X)={\int }_{-\infty }^{\infty }x{f}_{x}(x)dx$ 和 $E(Y)={\int }_{-\infty }^{\infty }y{f}_{y}(y)dy$。
步骤 4:求D(X)和D(Y)
根据方差的定义,我们有 $D(X)=E({X}^{2})-{[E(X)]}^{2}$ 和 $D(Y)=E({Y}^{2})-{[E(Y)]}^{2}$,其中 $E({X}^{2})={\int }_{-\infty }^{\infty }{x}^{2}{f}_{x}(x)dx$ 和 $E({Y}^{2})={\int }_{-\infty }^{\infty }{y}^{2}{f}_{y}(y)dy$。
步骤 5:求cov(X,Y)
根据协方差的定义,我们有 $cov(X,Y)=E(XY)-E(X)E(Y)$,其中 $E(XY)={\iint }_{-\infty }^{\infty }xyf(x,y)dxdy$。