题目
计算曲线积分siny+y+π)dx+(e^2cosy -x)dy-|||-L;式中L是从点A(1,0)经下半圆周siny+y+π)dx+(e^2cosy -x)dy-|||-L到点 B(3,0)
计算曲线积分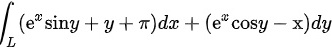 ;式中L是从点A(1,0)经下半圆周
;式中L是从点A(1,0)经下半圆周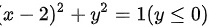 到点 B(3,0)
到点 B(3,0)
题目解答
答案
令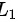 :x=0(1≤x≤3),
:x=0(1≤x≤3), 和L形成一个封闭区域
和L形成一个封闭区域
由格林公式
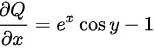 ,
,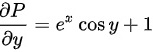
∴原式=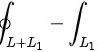
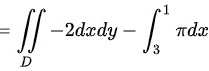
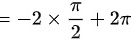
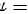
解析
步骤 1:确定积分路径
曲线积分的路径L是从点A(1,0)经下半圆周${(x-2)}^{2}+{y}^{2}=1(y\leqslant 0)$到点B(3,0)。为了应用格林公式,我们需要将L与一条直线L1(从B到A)一起形成一个封闭区域。
步骤 2:应用格林公式
格林公式表明,对于一个封闭区域D,其边界为L和L1,如果P和Q在D上具有连续的一阶偏导数,则有
${\int }_{L}^{Pdx+Qdy}+{\int }_{L1}^{Pdx+Qdy}={\iint }_{D}^{(\dfrac {\partial Q}{\partial x}-\dfrac {\partial P}{\partial y})dxdy$。
其中,$P={e}^{x}\sin y+y+\pi$,$Q={e}^{x}\cos y-x$。
步骤 3:计算偏导数
计算$\dfrac {\partial Q}{\partial x}$和$\dfrac {\partial P}{\partial y}$:
$\dfrac {\partial Q}{\partial x}={e}^{x}\cos y-1$,
$\dfrac {\partial P}{\partial y}={e}^{x}\cos y+1$。
步骤 4:计算封闭区域D上的二重积分
$\dfrac {\partial Q}{\partial x}-\dfrac {\partial P}{\partial y}=-2$,因此
${\iint }_{D}^{(\dfrac {\partial Q}{\partial x}-\dfrac {\partial P}{\partial y})dxdy}={\iint }_{D}^{-2dxdy}=-2\times \text{区域D的面积}$。
区域D的面积是半圆的面积,即$\dfrac {\pi }{2}$,所以
${\iint }_{D}^{-2dxdy}=-2\times \dfrac {\pi }{2}=-\pi$。
步骤 5:计算L1上的积分
L1是从B(3,0)到A(1,0)的直线,因此$dy=0$,$dx=-2$,所以
${\int }_{L1}^{Pdx+Qdy}={\int }_{3}^{1}({e}^{x}\sin y+y+\pi )dx={\int }_{3}^{1}(\pi )dx=2\pi$。
步骤 6:计算原曲线积分
原曲线积分等于封闭区域D上的二重积分加上L1上的积分,即
${\int }_{L}^{Pdx+Qdy}=-\pi+2\pi=\pi$。
曲线积分的路径L是从点A(1,0)经下半圆周${(x-2)}^{2}+{y}^{2}=1(y\leqslant 0)$到点B(3,0)。为了应用格林公式,我们需要将L与一条直线L1(从B到A)一起形成一个封闭区域。
步骤 2:应用格林公式
格林公式表明,对于一个封闭区域D,其边界为L和L1,如果P和Q在D上具有连续的一阶偏导数,则有
${\int }_{L}^{Pdx+Qdy}+{\int }_{L1}^{Pdx+Qdy}={\iint }_{D}^{(\dfrac {\partial Q}{\partial x}-\dfrac {\partial P}{\partial y})dxdy$。
其中,$P={e}^{x}\sin y+y+\pi$,$Q={e}^{x}\cos y-x$。
步骤 3:计算偏导数
计算$\dfrac {\partial Q}{\partial x}$和$\dfrac {\partial P}{\partial y}$:
$\dfrac {\partial Q}{\partial x}={e}^{x}\cos y-1$,
$\dfrac {\partial P}{\partial y}={e}^{x}\cos y+1$。
步骤 4:计算封闭区域D上的二重积分
$\dfrac {\partial Q}{\partial x}-\dfrac {\partial P}{\partial y}=-2$,因此
${\iint }_{D}^{(\dfrac {\partial Q}{\partial x}-\dfrac {\partial P}{\partial y})dxdy}={\iint }_{D}^{-2dxdy}=-2\times \text{区域D的面积}$。
区域D的面积是半圆的面积,即$\dfrac {\pi }{2}$,所以
${\iint }_{D}^{-2dxdy}=-2\times \dfrac {\pi }{2}=-\pi$。
步骤 5:计算L1上的积分
L1是从B(3,0)到A(1,0)的直线,因此$dy=0$,$dx=-2$,所以
${\int }_{L1}^{Pdx+Qdy}={\int }_{3}^{1}({e}^{x}\sin y+y+\pi )dx={\int }_{3}^{1}(\pi )dx=2\pi$。
步骤 6:计算原曲线积分
原曲线积分等于封闭区域D上的二重积分加上L1上的积分,即
${\int }_{L}^{Pdx+Qdy}=-\pi+2\pi=\pi$。