题目
设曲线L:f(x，y)=1(f(x，y)具有一阶连续偏导数)，过第二象限内的点M和第四象限内的点N，T为L上从点M到N的一段弧，则下列小于零的是( )A. ∫Tf(x，y)dxB. ∫Tf(x，y)dyC. ∫Tf(x，y)dsD. ∫Tf′x(x，y)dx+f′y(x，y)dy
设曲线L:f(x，y)=1(f(x，y)具有一阶连续偏导数)，过第二象限内的点M和第四象限内的点N，T为L上从点M到N的一段弧，则下列小于零的是( )
A. ∫Tf(x，y)dx
B. ∫Tf(x，y)dy
C. ∫Tf(x，y)ds
D. ∫Tf′x(x，y)dx+f′y(x，y)dy
A. ∫Tf(x，y)dx
B. ∫Tf(x，y)dy
C. ∫Tf(x，y)ds
D. ∫Tf′x(x，y)dx+f′y(x，y)dy
题目解答
答案
设M、N点的坐标分别为M(x1，y1)，N(x2，y2)，x1＜x2，y1＞y2．
将曲线方程代入积分表达式，再计算有：
对于选项A：
 |
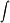| T |
|
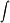| T |
对于选项B：
|
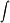| T |
|
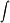| T |
对于选项C：
|
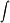| T |
|
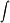| T |
对于选项D：
|
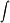| T |
|
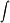| T |
故选：B．
解析
步骤 1：确定点M和N的坐标
设M、N点的坐标分别为M(x_1，y_1)，N(x_2，y_2)，x_1＜x_2，y_1＞y_2．
步骤 2：计算选项A的积分
将曲线方程代入积分表达式，再计算有：
对于选项A：
∫_Tf(x，y)dx＝∫_Tdx＝x_2−x_1＞0；
步骤 3：计算选项B的积分
对于选项B：
∫_Tf(x，y)dy＝∫_Tdy＝y_2−y_1＜0；
步骤 4：计算选项C的积分
对于选项C：
∫_Tf(x，y)ds＝∫_Tds＝s＞0；
步骤 5：计算选项D的积分
对于选项D：
∫_Tf′_x(x，y)dx+f′_y(x，y)dy＝∫_Tdf(x，y)＝0．
设M、N点的坐标分别为M(x_1，y_1)，N(x_2，y_2)，x_1＜x_2，y_1＞y_2．
步骤 2：计算选项A的积分
将曲线方程代入积分表达式，再计算有：
对于选项A：
∫_Tf(x，y)dx＝∫_Tdx＝x_2−x_1＞0；
步骤 3：计算选项B的积分
对于选项B：
∫_Tf(x，y)dy＝∫_Tdy＝y_2−y_1＜0；
步骤 4：计算选项C的积分
对于选项C：
∫_Tf(x，y)ds＝∫_Tds＝s＞0；
步骤 5：计算选项D的积分
对于选项D：
∫_Tf′_x(x，y)dx+f′_y(x，y)dy＝∫_Tdf(x，y)＝0．