题目
19.设f(x)连续,且 (int )_(0)^xtf(2x-t)dt=dfrac (1)(2)arctan (x)^2 (1)=1, 则 (int )_(1)^2f(x)dx= __
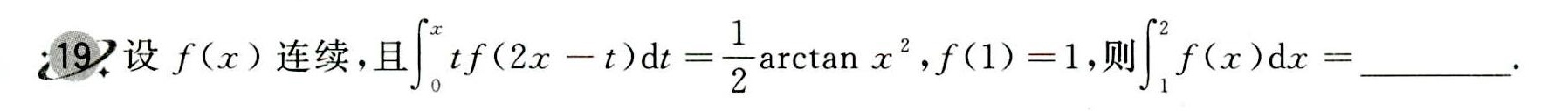
题目解答
答案
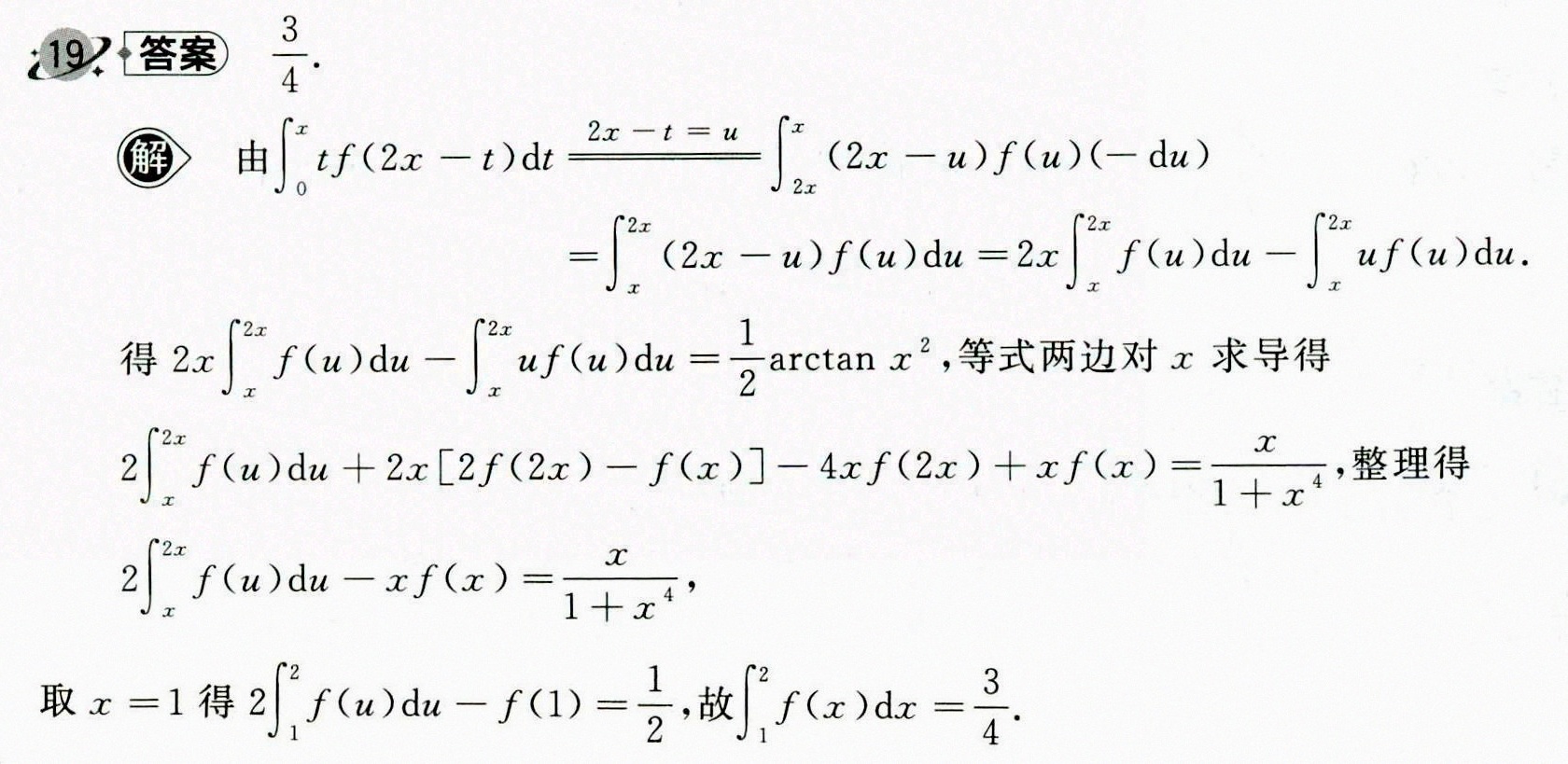
解析
步骤 1:代换变量
令 $u = 2x - t$,则 $t = 2x - u$,$dt = -du$。当 $t = 0$ 时,$u = 2x$;当 $t = x$ 时,$u = x$。因此,原积分可以写为:
$${\int }_{0}^{x}tf(2x-t)dt = {\int }_{2x}^{x}(2x-u)f(u)(-du) = {\int }_{x}^{2x}(2x-u)f(u)du$$
步骤 2:拆分积分
将上式拆分为两个积分:
$${\int }_{x}^{2x}(2x-u)f(u)du = 2x{\int }_{x}^{2x}f(u)du - {\int }_{x}^{2x}uf(u)du$$
步骤 3:等式两边对x求导
根据题目条件,有:
$$2x{\int }_{x}^{2x}f(u)du - {\int }_{x}^{2x}uf(u)du = \dfrac {1}{2}\arctan {x}^{2}$$
对上式两边对 $x$ 求导,得到:
$$2{\int }_{x}^{2x}f(u)du + 2x(2f(2x) - f(x)) - (2xf(2x) - xf(x)) = \dfrac {x}{1 + x^4}$$
化简得:
$$2{\int }_{x}^{2x}f(u)du - xf(x) = \dfrac {x}{1 + x^4}$$
步骤 4:代入x=1
将 $x = 1$ 代入上式,得到:
$$2{\int }_{1}^{2}f(u)du - f(1) = \dfrac {1}{2}$$
由于 $f(1) = 1$,则:
$$2{\int }_{1}^{2}f(u)du - 1 = \dfrac {1}{2}$$
解得:
$${\int }_{1}^{2}f(u)du = \dfrac {3}{4}$$
令 $u = 2x - t$,则 $t = 2x - u$,$dt = -du$。当 $t = 0$ 时,$u = 2x$;当 $t = x$ 时,$u = x$。因此,原积分可以写为:
$${\int }_{0}^{x}tf(2x-t)dt = {\int }_{2x}^{x}(2x-u)f(u)(-du) = {\int }_{x}^{2x}(2x-u)f(u)du$$
步骤 2:拆分积分
将上式拆分为两个积分:
$${\int }_{x}^{2x}(2x-u)f(u)du = 2x{\int }_{x}^{2x}f(u)du - {\int }_{x}^{2x}uf(u)du$$
步骤 3:等式两边对x求导
根据题目条件,有:
$$2x{\int }_{x}^{2x}f(u)du - {\int }_{x}^{2x}uf(u)du = \dfrac {1}{2}\arctan {x}^{2}$$
对上式两边对 $x$ 求导,得到:
$$2{\int }_{x}^{2x}f(u)du + 2x(2f(2x) - f(x)) - (2xf(2x) - xf(x)) = \dfrac {x}{1 + x^4}$$
化简得:
$$2{\int }_{x}^{2x}f(u)du - xf(x) = \dfrac {x}{1 + x^4}$$
步骤 4:代入x=1
将 $x = 1$ 代入上式,得到:
$$2{\int }_{1}^{2}f(u)du - f(1) = \dfrac {1}{2}$$
由于 $f(1) = 1$,则:
$$2{\int }_{1}^{2}f(u)du - 1 = \dfrac {1}{2}$$
解得:
$${\int }_{1}^{2}f(u)du = \dfrac {3}{4}$$