题目
设=arctan dfrac (x)(y),则在点(0,1)处的全微分=arctan dfrac (x)(y)__________.
设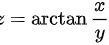 ,则在点(0,1)处的全微分
,则在点(0,1)处的全微分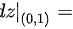 __________.
__________.
题目解答
答案
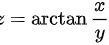 ,则对x,y分别求偏导,得
,则对x,y分别求偏导,得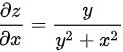 ,
,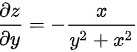
∴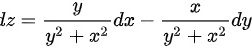
∴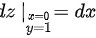
解析
步骤 1:求偏导数
对函数$z=\arctan \dfrac {x}{y}$,分别对$x$和$y$求偏导数。根据$\arctan$函数的导数公式,我们有:
$$\dfrac {\partial z}{\partial x}=\dfrac {1}{1+(\dfrac {x}{y})^2} \cdot \dfrac {1}{y}=\dfrac {y}{{y}^{2}+{x}^{2}}$$
$$\dfrac {\partial z}{\partial y}=\dfrac {1}{1+(\dfrac {x}{y})^2} \cdot (-\dfrac {x}{{y}^{2}})=-\dfrac {x}{{y}^{2}+{x}^{2}}$$
步骤 2:代入点(0,1)
将点(0,1)代入上述偏导数中,得到:
$$\dfrac {\partial z}{\partial x}|_{(0,1)}=\dfrac {1}{{1}^{2}+{0}^{2}}=1$$
$$\dfrac {\partial z}{\partial y}|_{(0,1)}=-\dfrac {0}{{1}^{2}+{0}^{2}}=0$$
步骤 3:计算全微分
根据全微分的定义,我们有:
$$dz=\dfrac {\partial z}{\partial x}dx+\dfrac {\partial z}{\partial y}dy$$
将步骤2中得到的偏导数代入,得到:
$$dz|_{(0,1)}=1\cdot dx+0\cdot dy=dx$$
对函数$z=\arctan \dfrac {x}{y}$,分别对$x$和$y$求偏导数。根据$\arctan$函数的导数公式,我们有:
$$\dfrac {\partial z}{\partial x}=\dfrac {1}{1+(\dfrac {x}{y})^2} \cdot \dfrac {1}{y}=\dfrac {y}{{y}^{2}+{x}^{2}}$$
$$\dfrac {\partial z}{\partial y}=\dfrac {1}{1+(\dfrac {x}{y})^2} \cdot (-\dfrac {x}{{y}^{2}})=-\dfrac {x}{{y}^{2}+{x}^{2}}$$
步骤 2:代入点(0,1)
将点(0,1)代入上述偏导数中,得到:
$$\dfrac {\partial z}{\partial x}|_{(0,1)}=\dfrac {1}{{1}^{2}+{0}^{2}}=1$$
$$\dfrac {\partial z}{\partial y}|_{(0,1)}=-\dfrac {0}{{1}^{2}+{0}^{2}}=0$$
步骤 3:计算全微分
根据全微分的定义,我们有:
$$dz=\dfrac {\partial z}{\partial x}dx+\dfrac {\partial z}{\partial y}dy$$
将步骤2中得到的偏导数代入,得到:
$$dz|_{(0,1)}=1\cdot dx+0\cdot dy=dx$$