题目
设L为椭圆dfrac ({x)^2}(2)+dfrac ({y)^2}(3)=1，其周长为a，则dfrac ({x)^2}(2)+dfrac ({y)^2}(3)=1（）。 A. a B. 3a C. 6a D. 12a
设L为椭圆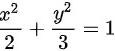
，其周长为a，则
（）。
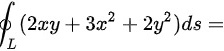A. a
B. 3a
C. 6a
D. 12a
题目解答
答案
∵椭圆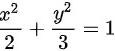，而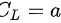
∵L关于x、y轴对称
∴由对称性可知，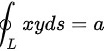
∴
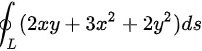
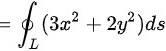
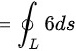
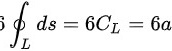
故答案为：C。
解析
步骤 1：理解椭圆的参数方程
椭圆$\dfrac{{x}^{2}}{2}+\dfrac{{y}^{2}}{3}=1$的参数方程可以表示为$x=\sqrt{2}\cos\theta$，$y=\sqrt{3}\sin\theta$，其中$\theta$为参数，范围为$[0,2\pi]$。
步骤 2：计算椭圆的周长
椭圆的周长$a$可以通过椭圆积分计算，但这里直接给出周长为$a$。
步骤 3：计算积分
根据对称性，$xyds$的积分结果为0，因为椭圆关于x轴和y轴对称，所以$xy$的正负值会相互抵消。因此，$\int (2xy+3{x}^{2}+2{y}^{2})ds$可以简化为$\int (3{x}^{2}+2{y}^{2})ds$。
步骤 4：计算$3{x}^{2}+2{y}^{2}$的积分
将$x=\sqrt{2}\cos\theta$，$y=\sqrt{3}\sin\theta$代入$3{x}^{2}+2{y}^{2}$，得到$3(\sqrt{2}\cos\theta)^{2}+2(\sqrt{3}\sin\theta)^{2}=6\cos^{2}\theta+6\sin^{2}\theta=6$。因此，$\int (3{x}^{2}+2{y}^{2})ds=6\int ds=6a$。
椭圆$\dfrac{{x}^{2}}{2}+\dfrac{{y}^{2}}{3}=1$的参数方程可以表示为$x=\sqrt{2}\cos\theta$，$y=\sqrt{3}\sin\theta$，其中$\theta$为参数，范围为$[0,2\pi]$。
步骤 2：计算椭圆的周长
椭圆的周长$a$可以通过椭圆积分计算，但这里直接给出周长为$a$。
步骤 3：计算积分
根据对称性，$xyds$的积分结果为0，因为椭圆关于x轴和y轴对称，所以$xy$的正负值会相互抵消。因此，$\int (2xy+3{x}^{2}+2{y}^{2})ds$可以简化为$\int (3{x}^{2}+2{y}^{2})ds$。
步骤 4：计算$3{x}^{2}+2{y}^{2}$的积分
将$x=\sqrt{2}\cos\theta$，$y=\sqrt{3}\sin\theta$代入$3{x}^{2}+2{y}^{2}$，得到$3(\sqrt{2}\cos\theta)^{2}+2(\sqrt{3}\sin\theta)^{2}=6\cos^{2}\theta+6\sin^{2}\theta=6$。因此，$\int (3{x}^{2}+2{y}^{2})ds=6\int ds=6a$。