题目
计算二重积分xydxdy,其中xydxdy是由曲线xydxdy以及xydxdy轴所围成的闭区域。
计算二重积分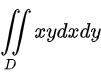 ,其中
,其中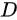 是由曲线
是由曲线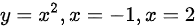 以及
以及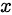 轴所围成的闭区域。
轴所围成的闭区域。
题目解答
答案
因为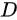 是由曲线
是由曲线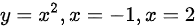 以及
以及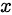 轴所围成的闭区域,
轴所围成的闭区域,
所以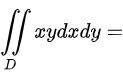
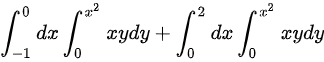
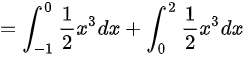
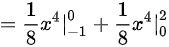
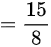
解析
步骤 1:确定积分区域
由曲线$y={x}^{2}$,$x=-1$,$x=2$以及轴所围成的闭区域,可以确定积分区域D为$-1\leq x\leq 2$,$0\leq y\leq {x}^{2}$。
步骤 2:设置二重积分
根据积分区域D,设置二重积分${\iint }_{D}xydxdy$。
步骤 3:计算二重积分
将二重积分转化为累次积分,即${\iint }_{D}xydxdy={\int }_{-1}^{2}dx{\int }_{0}^{{x}^{2}}xydy$。
步骤 4:计算内层积分
计算内层积分${\int }_{0}^{{x}^{2}}xydy$,得到$\dfrac {1}{2}{x}^{3}$。
步骤 5:计算外层积分
计算外层积分${\int }_{-1}^{2}\dfrac {1}{2}{x}^{3}dx$,得到$\dfrac {1}{8}{x}^{4}{|}_{-1}^{2}$。
步骤 6:计算最终结果
计算最终结果$\dfrac {1}{8}{x}^{4}{|}_{-1}^{2}$,得到$\dfrac {15}{8}$。
由曲线$y={x}^{2}$,$x=-1$,$x=2$以及轴所围成的闭区域,可以确定积分区域D为$-1\leq x\leq 2$,$0\leq y\leq {x}^{2}$。
步骤 2:设置二重积分
根据积分区域D,设置二重积分${\iint }_{D}xydxdy$。
步骤 3:计算二重积分
将二重积分转化为累次积分,即${\iint }_{D}xydxdy={\int }_{-1}^{2}dx{\int }_{0}^{{x}^{2}}xydy$。
步骤 4:计算内层积分
计算内层积分${\int }_{0}^{{x}^{2}}xydy$,得到$\dfrac {1}{2}{x}^{3}$。
步骤 5:计算外层积分
计算外层积分${\int }_{-1}^{2}\dfrac {1}{2}{x}^{3}dx$,得到$\dfrac {1}{8}{x}^{4}{|}_{-1}^{2}$。
步骤 6:计算最终结果
计算最终结果$\dfrac {1}{8}{x}^{4}{|}_{-1}^{2}$,得到$\dfrac {15}{8}$。