题目
求极限lim _(narrow infty )dfrac ({5)^n+(2)^n}({5)^n-(3)^n}
求极限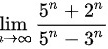
题目解答
答案
原式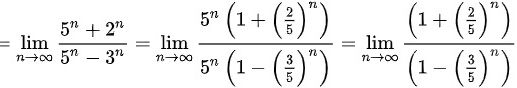
∵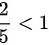
∴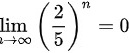
同理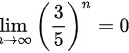
∴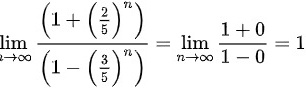
解析
步骤 1:提取公因式
提取公因式${5}^{n}$,将分子和分母都除以${5}^{n}$,得到$\lim _{n\rightarrow \infty }\dfrac {1+{(\dfrac {2}{5})}^{n}}{1-{(\dfrac {3}{5})}^{n}}$。
步骤 2:分析指数函数的极限
由于$\dfrac {2}{5}\lt 1$和$\dfrac {3}{5}\lt 1$,当$n\rightarrow \infty$时,${(\dfrac {2}{5})}^{n}\rightarrow 0$和${(\dfrac {3}{5})}^{n}\rightarrow 0$。
步骤 3:计算极限
将步骤2的结果代入步骤1的表达式中,得到$\lim _{n\rightarrow \infty }\dfrac {1+0}{1-0}=1$。
提取公因式${5}^{n}$,将分子和分母都除以${5}^{n}$,得到$\lim _{n\rightarrow \infty }\dfrac {1+{(\dfrac {2}{5})}^{n}}{1-{(\dfrac {3}{5})}^{n}}$。
步骤 2:分析指数函数的极限
由于$\dfrac {2}{5}\lt 1$和$\dfrac {3}{5}\lt 1$,当$n\rightarrow \infty$时,${(\dfrac {2}{5})}^{n}\rightarrow 0$和${(\dfrac {3}{5})}^{n}\rightarrow 0$。
步骤 3:计算极限
将步骤2的结果代入步骤1的表达式中,得到$\lim _{n\rightarrow \infty }\dfrac {1+0}{1-0}=1$。