题目
求微分方程 ydx+(y-x)dy=0 的通解.
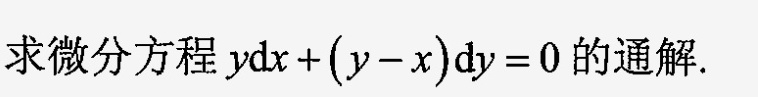
题目解答
答案
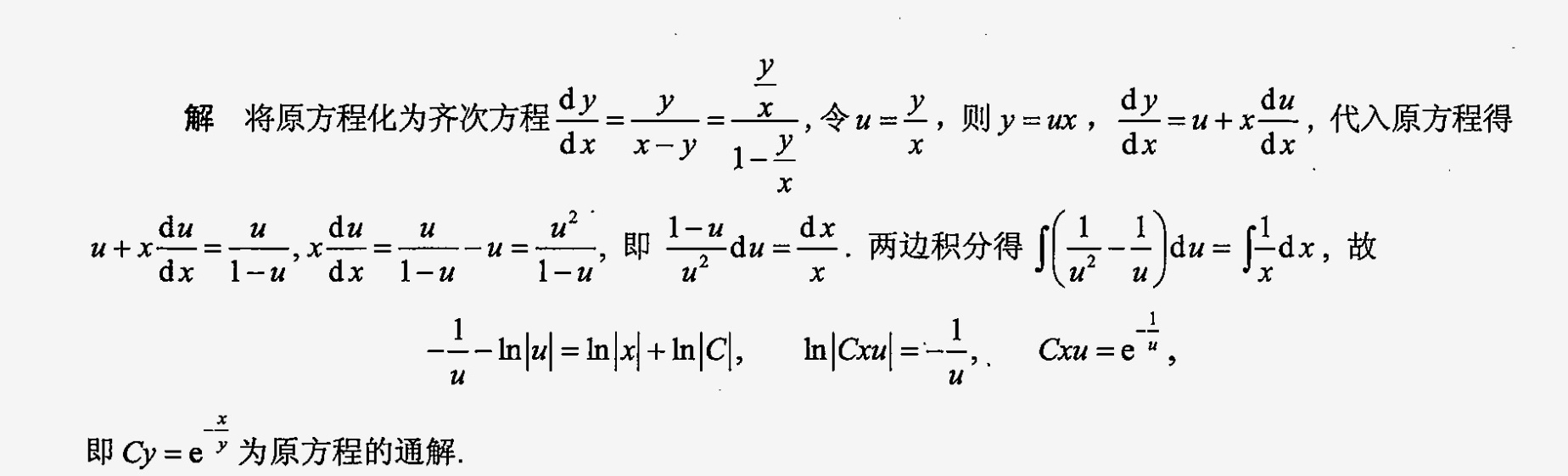
解析
步骤 1:将原方程化为齐次方程
原方程为 $ydx+(y-x)dy=0$,可以改写为 $\dfrac{dy}{dx}=\dfrac{y}{x-y}$。为了将方程化为齐次方程,我们引入变量 $u=\dfrac{y}{x}$,即 $y=ux$。这样,原方程可以表示为 $\dfrac{dy}{dx}=\dfrac{u}{1-u}$。
步骤 2:代入变量 $u$ 并求解
由于 $y=ux$,则 $\dfrac{dy}{dx}=u+x\dfrac{du}{dx}$。将这个表达式代入原方程,得到 $u+x\dfrac{du}{dx}=\dfrac{u}{1-u}$。整理得到 $x\dfrac{du}{dx}=\dfrac{u}{1-u}-u=\dfrac{u^2}{1-u}$。因此,我们得到 $\dfrac{1-u}{u^2}du=\dfrac{dx}{x}$。
步骤 3:积分求解
对两边积分,得到 $\int (\dfrac{1}{u^2}-\dfrac{1}{u})du=\int \dfrac{1}{x}dx$。积分后得到 $-\dfrac{1}{u}-\ln|u|=\ln|x|+\ln|C|$,即 $\ln|Cxu|=-\dfrac{1}{u}$。因此,$Cxu=e^{-\dfrac{1}{u}}$,即 $Cy=e^{-\dfrac{x}{y}}$。
原方程为 $ydx+(y-x)dy=0$,可以改写为 $\dfrac{dy}{dx}=\dfrac{y}{x-y}$。为了将方程化为齐次方程,我们引入变量 $u=\dfrac{y}{x}$,即 $y=ux$。这样,原方程可以表示为 $\dfrac{dy}{dx}=\dfrac{u}{1-u}$。
步骤 2:代入变量 $u$ 并求解
由于 $y=ux$,则 $\dfrac{dy}{dx}=u+x\dfrac{du}{dx}$。将这个表达式代入原方程,得到 $u+x\dfrac{du}{dx}=\dfrac{u}{1-u}$。整理得到 $x\dfrac{du}{dx}=\dfrac{u}{1-u}-u=\dfrac{u^2}{1-u}$。因此,我们得到 $\dfrac{1-u}{u^2}du=\dfrac{dx}{x}$。
步骤 3:积分求解
对两边积分,得到 $\int (\dfrac{1}{u^2}-\dfrac{1}{u})du=\int \dfrac{1}{x}dx$。积分后得到 $-\dfrac{1}{u}-\ln|u|=\ln|x|+\ln|C|$,即 $\ln|Cxu|=-\dfrac{1}{u}$。因此,$Cxu=e^{-\dfrac{1}{u}}$,即 $Cy=e^{-\dfrac{x}{y}}$。