题目
甲乙两人约定星期日早晨7时到8时之间到某公共汽车站乘车,假定甲乙到达车站的时刻是互不相干的,且每人在7时到8时这段时间内任何时刻到达车站是等可能的。已知在这段时间内有四班公共汽车,它们的开车时刻分别为 7:15 , 7:30 , 7:45 , 8:00, 若甲乙约定“车来就乘,彼此不等”,求甲、乙同乘一班车的概率。
甲乙两人约定星期日早晨7时到8时之间到某公共汽车站乘车,假定甲乙到达车站的时刻是互不相干的,且每人在7时到8时这段时间内任何时刻到达车站是等可能的。已知在这段时间内有四班公共汽车,它们的开车时刻分别为 7:15 , 7:30 , 7:45 , 8:00, 若甲乙约定“车来就乘,彼此不等”,求甲、乙同乘一班车的概率。
题目解答
答案
他们乘车的可能总结果数为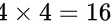 种,同乘一班车的结果数为4种:开车时刻分别为7:15 , 7:30 , 7:45 , 8:00的四班车。以上分析如下图所示:
种,同乘一班车的结果数为4种:开车时刻分别为7:15 , 7:30 , 7:45 , 8:00的四班车。以上分析如下图所示:
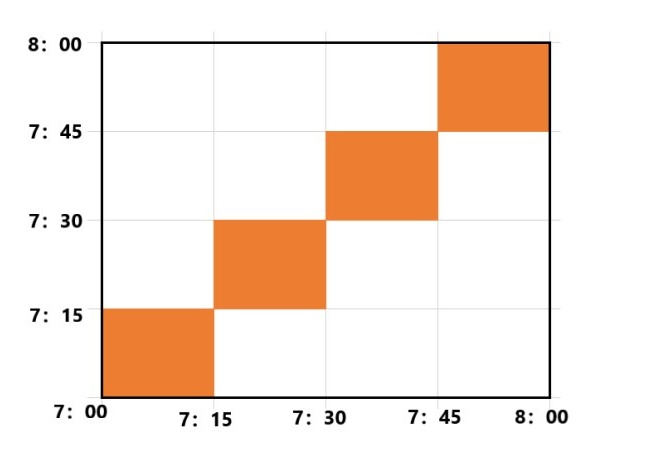
有古典概型的值甲乙同乘一班车的概率为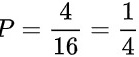
因此,若甲乙约定“车来就乘,彼此不等”,甲、乙同乘一班车的概率为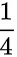 。
。
解析
考查要点:本题主要考查几何概率模型的应用,涉及独立事件和等可能条件的理解。
解题核心思路:
- 时间区间划分:根据发车时刻将1小时划分为4个等长的15分钟区间,每个区间对应一班车。
- 独立性分析:甲、乙到达时间相互独立,且每个时间区间被选中的概率相等。
- 概率计算:通过计算甲、乙到达时间落在同一区间的情况数占总情况数的比例,得到最终概率。
破题关键点:
- 等长区间:每个发车间隔为15分钟,保证每个班车被选中的概率相同。
- 几何模型:将甲、乙到达时间看作平面直角坐标系中的点,总情况对应边长为60的正方形,符合条件的区域为4个边长为15的正方形。
步骤1:划分时间区间
将7:00到8:00划分为4个15分钟的区间:
- 7:15班车:到达时间在$[0,15)$分钟
- 7:30班车:到达时间在$[15,30)$分钟
- 7:45班车:到达时间在$[30,45)$分钟
- 8:00班车:到达时间在$[45,60]$分钟
步骤2:建立几何模型
- 甲、乙到达时间分别用$x$和$y$表示,取值范围均为$[0,60]$。
- 总情况对应坐标系中边长为60的正方形区域,面积为$60 \times 60 = 3600$。
步骤3:计算符合条件的区域
甲、乙同乘一班车的条件是$x$和$y$落在同一区间内:
- 每个区间对应的小正方形面积:边长为15,面积为$15 \times 15 = 225$。
- 总符合条件区域面积:$4 \times 225 = 900$。
步骤4:计算概率
概率为符合条件区域面积与总面积的比值:
$P = \frac{900}{3600} = \frac{1}{4}$