题目
点 x=0 ()是函数 =(x)^4 的 () 。A、驻点但非极值点B、拐点C、驻点且是拐点D、驻点且是极值点
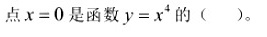
- A、驻点但非极值点
- B、拐点
- C、驻点且是拐点
- D、驻点且是极值点
题目解答
答案
D. 驻点且是极值点
解析
步骤 1:求导数
首先,我们需要求出函数 $y = x^4$ 的一阶导数和二阶导数,以确定点 $x=0$ 的性质。
一阶导数:$y' = 4x^3$
二阶导数:$y'' = 12x^2$
步骤 2:判断驻点
驻点是指函数的一阶导数为零的点。将 $x=0$ 代入一阶导数 $y' = 4x^3$,得到 $y'(0) = 0$,因此 $x=0$ 是函数的驻点。
步骤 3:判断极值点
极值点是指函数的一阶导数为零且二阶导数不为零的点。将 $x=0$ 代入二阶导数 $y'' = 12x^2$,得到 $y''(0) = 0$。由于二阶导数在 $x=0$ 处也为零,我们需要进一步判断。观察函数 $y = x^4$ 的图像,可以看出 $x=0$ 是函数的极小值点。
步骤 4:判断拐点
拐点是指函数的二阶导数为零且二阶导数在该点两侧符号不同的点。由于 $y'' = 12x^2$ 在 $x=0$ 两侧均为正,因此 $x=0$ 不是函数的拐点。
首先,我们需要求出函数 $y = x^4$ 的一阶导数和二阶导数,以确定点 $x=0$ 的性质。
一阶导数:$y' = 4x^3$
二阶导数:$y'' = 12x^2$
步骤 2:判断驻点
驻点是指函数的一阶导数为零的点。将 $x=0$ 代入一阶导数 $y' = 4x^3$,得到 $y'(0) = 0$,因此 $x=0$ 是函数的驻点。
步骤 3:判断极值点
极值点是指函数的一阶导数为零且二阶导数不为零的点。将 $x=0$ 代入二阶导数 $y'' = 12x^2$,得到 $y''(0) = 0$。由于二阶导数在 $x=0$ 处也为零,我们需要进一步判断。观察函数 $y = x^4$ 的图像,可以看出 $x=0$ 是函数的极小值点。
步骤 4:判断拐点
拐点是指函数的二阶导数为零且二阶导数在该点两侧符号不同的点。由于 $y'' = 12x^2$ 在 $x=0$ 两侧均为正,因此 $x=0$ 不是函数的拐点。