题目
装有20件某产品(其中一等品10件,二等品5件,三等品5件)的箱子中丢失一件产品,但不知是几等品,今从箱中任取2件产品,计算:(1)两件都是一等品的概率;(2)若两件都是一等品,求丢失的也是一等品的概率。
装有20件某产品(其中一等品10件,二等品5件,三等品5件)的箱子中丢失一件产品,但不知是几等品,今从箱中任取2件产品,计算:
(1)两件都是一等品的概率;
(2)若两件都是一等品,求丢失的也是一等品的概率。
题目解答
答案
(1)分为两种情况
丢失的是一等品的情况下,取出两件都是一等品的概率为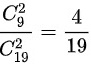 ;
;
丢失的不是一等品的情况下,取出两件都是一等品的概率为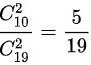 ;
;
∴两件都是一等品的概率为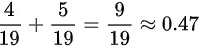
(2)由(1)知在丢失的是一等品的情况下,取出两件都是一等品的概率为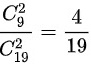 ;
;
丢失的是一等品的概率为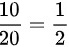
∴若两件都是一等品,求丢失的也是一等品的概率为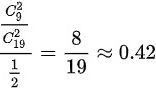
故答案为(1)0.47
(2)0.42
解析
步骤 1:计算丢失一等品时,取出两件都是一等品的概率
丢失一等品后,箱子里剩下19件产品,其中一等品9件。从这19件产品中任取2件,都是从9件一等品中取出,所以概率为$\dfrac{{C}_{9}^{2}}{{C}_{19}^{2}}$。
步骤 2:计算丢失非一等品时,取出两件都是一等品的概率
丢失非一等品后,箱子里剩下19件产品,其中一等品10件。从这19件产品中任取2件,都是从10件一等品中取出,所以概率为$\dfrac{{C}_{10}^{2}}{{C}_{19}^{2}}$。
步骤 3:计算两件都是一等品的总概率
两件都是一等品的总概率为丢失一等品时的概率加上丢失非一等品时的概率,即$\dfrac{{C}_{9}^{2}}{{C}_{19}^{2}} + \dfrac{{C}_{10}^{2}}{{C}_{19}^{2}}$。
步骤 4:计算丢失一等品的条件概率
丢失一等品的条件概率为丢失一等品时取出两件都是一等品的概率除以两件都是一等品的总概率,即$\dfrac{\dfrac{{C}_{9}^{2}}{{C}_{19}^{2}}}{\dfrac{{C}_{9}^{2}}{{C}_{19}^{2}} + \dfrac{{C}_{10}^{2}}{{C}_{19}^{2}}}$。
丢失一等品后,箱子里剩下19件产品,其中一等品9件。从这19件产品中任取2件,都是从9件一等品中取出,所以概率为$\dfrac{{C}_{9}^{2}}{{C}_{19}^{2}}$。
步骤 2:计算丢失非一等品时,取出两件都是一等品的概率
丢失非一等品后,箱子里剩下19件产品,其中一等品10件。从这19件产品中任取2件,都是从10件一等品中取出,所以概率为$\dfrac{{C}_{10}^{2}}{{C}_{19}^{2}}$。
步骤 3:计算两件都是一等品的总概率
两件都是一等品的总概率为丢失一等品时的概率加上丢失非一等品时的概率,即$\dfrac{{C}_{9}^{2}}{{C}_{19}^{2}} + \dfrac{{C}_{10}^{2}}{{C}_{19}^{2}}$。
步骤 4:计算丢失一等品的条件概率
丢失一等品的条件概率为丢失一等品时取出两件都是一等品的概率除以两件都是一等品的总概率,即$\dfrac{\dfrac{{C}_{9}^{2}}{{C}_{19}^{2}}}{\dfrac{{C}_{9}^{2}}{{C}_{19}^{2}} + \dfrac{{C}_{10}^{2}}{{C}_{19}^{2}}}$。