题目
设f(x)有连续的导数, (0)=0,设f(x)有连续的导数, (0)=0,


题目解答
答案
解析: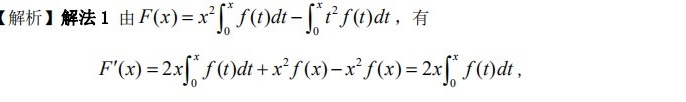

解析
考查要点:本题主要考查积分上限函数的求导法则、泰勒展开的应用以及无穷小阶数的判断。
解题核心思路:
- 积分求导:利用莱布尼茨规则对积分上限函数求导,将原积分拆分为两个积分后分别求导。
- 泰勒展开:由于$f(0)=0$,将$f(t)$展开为$f(t)=f'(0)t + o(t)$,简化积分表达式。
- 阶数分析:通过分析积分结果的阶数,确定$F'(x)$的阶数,从而找到与$x^k$同阶的$k$值。
破题关键点:
- 拆分积分:将原积分拆分为$x^2\int_0^x f(t)dt - \int_0^x t^2 f(t)dt$,简化求导过程。
- 泰勒展开:利用$f(0)=0$的条件展开$f(t)$,忽略高阶无穷小后,积分结果的阶数由$f'(0)t$主导。
- 阶数匹配:通过积分结果的阶数推导$F'(x)$的阶数,最终确定$k$的值。
步骤1:求导$F(x)$
根据莱布尼茨积分法则:
$F(x) = \int_0^x (x^2 - t^2)f(t)dt = x^2 \int_0^x f(t)dt - \int_0^x t^2 f(t)dt$
对$F(x)$求导:
$F'(x) = 2x \int_0^x f(t)dt + x^2 f(x) - x^2 f(x) = 2x \int_0^x f(t)dt$
步骤2:分析积分$\int_0^x f(t)dt$的阶数
由于$f(0)=0$且$f'(0) \neq 0$,对$f(t)$进行泰勒展开:
$f(t) = f(0) + f'(0)t + o(t) = f'(0)t + o(t)$
忽略高阶无穷小后,积分近似为:
$\int_0^x f(t)dt \approx \int_0^x f'(0)t \, dt = \frac{f'(0)}{2}x^2$
因此,$\int_0^x f(t)dt$是$x^2$的阶。
步骤3:确定$F'(x)$的阶数
将积分结果代入$F'(x)$:
$F'(x) = 2x \cdot \frac{f'(0)}{2}x^2 = f'(0)x^3$
因此,$F'(x)$是$x^3$的阶,即当$x \to 0$时,$F'(x) \sim f'(0)x^3$,故$k=3$。