题目
已知=(e)^-3x是微分方程=(e)^-3x的一个解，求=(e)^-3x的值及此微分方程的通解。
已知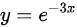
是微分方程
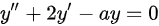的一个解，求
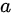的值及此微分方程的通解。
题目解答
答案
由于微分方程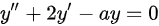的特征方程为
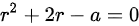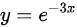。又是微分方程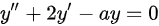的一个解，则其中一个特征根为
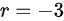。故
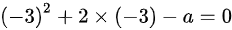，解得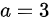
则特征方程为
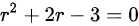，解得特征根为
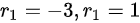。则此微分方程的通解为
。
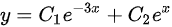解析
步骤 1：确定特征方程
微分方程${y}^{11}+2y'-ay=0$的特征方程为${r}^{2}+2r-a=0$。
步骤 2：利用已知解确定特征根
由于$y={e}^{-3x}$是微分方程${y}^{11}+2y'-ay=0$的一个解，因此特征方程的一个根为$r=-3$。
步骤 3：求解特征方程中的未知数a
将$r=-3$代入特征方程${r}^{2}+2r-a=0$，得到${(-3)}^{2}+2\times (-3)-a=0$，解得$a=3$。
步骤 4：求解特征方程
将$a=3$代入特征方程${r}^{2}+2r-a=0$，得到${r}^{2}+2r-3=0$，解得特征根为${r}_{1}=-3$和${r}_{2}=1$。
步骤 5：写出微分方程的通解
根据特征根${r}_{1}=-3$和${r}_{2}=1$，微分方程的通解为$y={C}_{1}{e}^{-3x}+{C}_{2}{e}^{x}$，其中${C}_{1}$和${C}_{2}$为任意常数。
微分方程${y}^{11}+2y'-ay=0$的特征方程为${r}^{2}+2r-a=0$。
步骤 2：利用已知解确定特征根
由于$y={e}^{-3x}$是微分方程${y}^{11}+2y'-ay=0$的一个解，因此特征方程的一个根为$r=-3$。
步骤 3：求解特征方程中的未知数a
将$r=-3$代入特征方程${r}^{2}+2r-a=0$，得到${(-3)}^{2}+2\times (-3)-a=0$，解得$a=3$。
步骤 4：求解特征方程
将$a=3$代入特征方程${r}^{2}+2r-a=0$，得到${r}^{2}+2r-3=0$，解得特征根为${r}_{1}=-3$和${r}_{2}=1$。
步骤 5：写出微分方程的通解
根据特征根${r}_{1}=-3$和${r}_{2}=1$，微分方程的通解为$y={C}_{1}{e}^{-3x}+{C}_{2}{e}^{x}$，其中${C}_{1}$和${C}_{2}$为任意常数。