题目
设=f(sin y,(e)^x+y) , 且=f(sin y,(e)^x+y)具有二阶连续偏导数, 求二阶偏导数=f(sin y,(e)^x+y).
设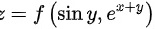 , 且
, 且 具有二阶连续偏导数, 求二阶偏导数
具有二阶连续偏导数, 求二阶偏导数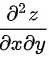 .
.
题目解答
答案
设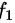 表示
表示 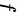 对其第一个参数求偏导数,
对其第一个参数求偏导数,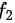 表示
表示 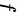 对其第二个参数求偏导数,先求
对其第二个参数求偏导数,先求 关于
关于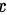 的偏导,将
的偏导,将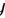 看成常量,得
看成常量,得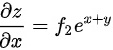 ,然后再对
,然后再对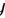 求偏导,得
求偏导,得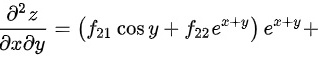
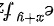
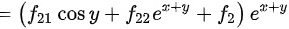
故本题的答案为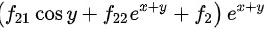
解析
步骤 1:定义偏导数符号
设$f_1$表示$f$对其第一个参数求偏导数,$f_2$表示$f$对其第二个参数求偏导数。
步骤 2:求关于$x$的偏导数
将$y$看成常量,对$z=f(\sin y, e^{x+y})$求关于$x$的偏导数,得$\dfrac{\partial z}{\partial x} = f_2 e^{x+y}$。
步骤 3:求关于$y$的偏导数
对$\dfrac{\partial z}{\partial x}$求关于$y$的偏导数,得$\dfrac{\partial^2 z}{\partial x \partial y} = (f_{21} \cos y + f_{22} e^{x+y}) e^{x+y} + e^{x+y} f_2$。
步骤 4:化简结果
化简$\dfrac{\partial^2 z}{\partial x \partial y}$,得$\dfrac{\partial^2 z}{\partial x \partial y} = (f_{21} \cos y + f_{22} e^{x+y} + f_2) e^{x+y}$。
设$f_1$表示$f$对其第一个参数求偏导数,$f_2$表示$f$对其第二个参数求偏导数。
步骤 2:求关于$x$的偏导数
将$y$看成常量,对$z=f(\sin y, e^{x+y})$求关于$x$的偏导数,得$\dfrac{\partial z}{\partial x} = f_2 e^{x+y}$。
步骤 3:求关于$y$的偏导数
对$\dfrac{\partial z}{\partial x}$求关于$y$的偏导数,得$\dfrac{\partial^2 z}{\partial x \partial y} = (f_{21} \cos y + f_{22} e^{x+y}) e^{x+y} + e^{x+y} f_2$。
步骤 4:化简结果
化简$\dfrac{\partial^2 z}{\partial x \partial y}$,得$\dfrac{\partial^2 z}{\partial x \partial y} = (f_{21} \cos y + f_{22} e^{x+y} + f_2) e^{x+y}$。