计算下列二重积分:-|||-(int )_(0)^1(x)^5dx(int )_({x)^2}^1(e)^-(y^2)dy

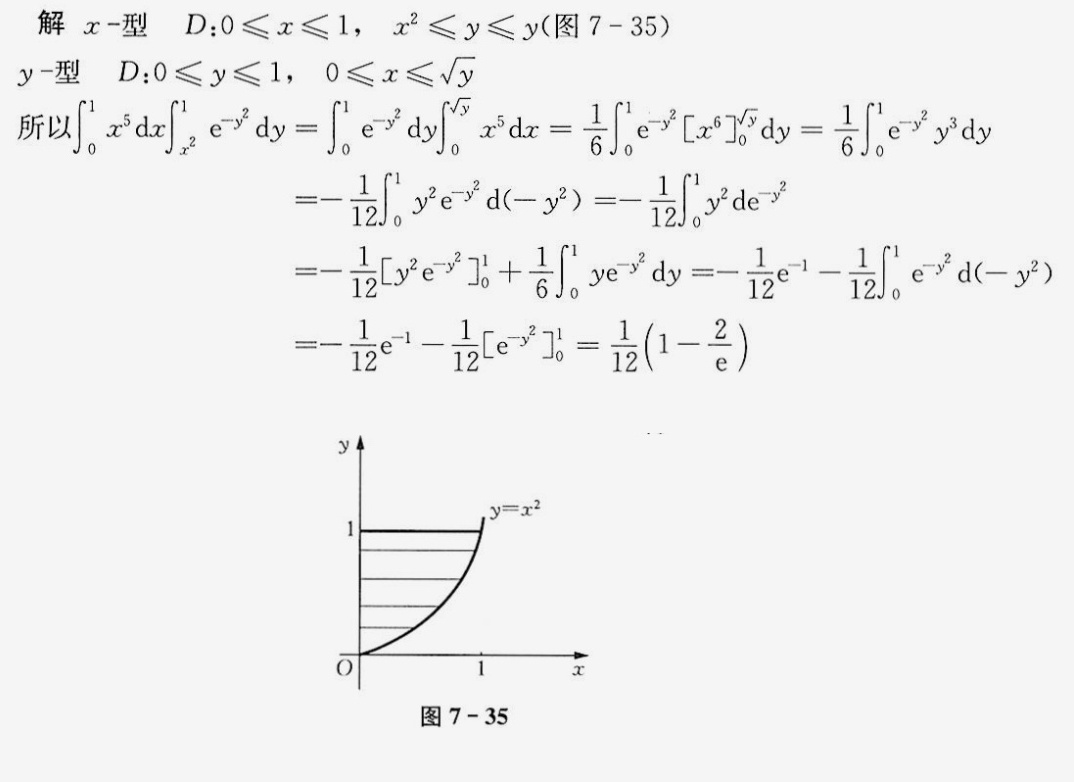
步骤 1：确定积分区域
首先，确定积分区域D。根据题目，积分区域D由$0\leqslant x\leqslant 1$和${x}^{2}\leqslant y\leqslant 1$定义。这意味着x的取值范围是0到1，而y的取值范围是$x^2$到1。

步骤 2：转换为y型积分
为了简化计算，将积分区域D转换为y型，即$0\leqslant y\leqslant 1$和$0\leqslant x\leqslant \sqrt{y}$。这样，原二重积分可以写为${\int }_{0}^{1}{\int }_{0}^{\sqrt{y}}{x}^{5}{e}^{-{y}^{2}}dxdy$。

步骤 3：计算内层积分
计算内层积分${\int }_{0}^{\sqrt{y}}{x}^{5}dx$。这是一个关于x的定积分，可以使用幂函数的积分公式${\int }_{a}^{b}{x}^{n}dx=\frac{{x}^{n+1}}{n+1}{|}_{a}^{b}$来计算。因此，${\int }_{0}^{\sqrt{y}}{x}^{5}dx=\frac{{x}^{6}}{6}{|}_{0}^{\sqrt{y}}=\frac{{(\sqrt{y})}^{6}}{6}=\frac{{y}^{3}}{6}$。

步骤 4：计算外层积分
将内层积分的结果代入外层积分，得到${\int }_{0}^{1}\frac{{y}^{3}}{6}{e}^{-{y}^{2}}dy$。这是一个关于y的定积分，可以使用分部积分法来计算。设$u={y}^{3}$，$dv={e}^{-{y}^{2}}dy$，则$du=3{y}^{2}dy$，$v=-\frac{1}{2}{e}^{-{y}^{2}}$。因此，${\int }_{0}^{1}\frac{{y}^{3}}{6}{e}^{-{y}^{2}}dy=\frac{1}{6}[-\frac{1}{2}{y}^{3}{e}^{-{y}^{2}}{|}_{0}^{1}+\frac{3}{2}{\int }_{0}^{1}{y}^{2}{e}^{-{y}^{2}}dy]$。

步骤 5：计算剩余积分
计算剩余积分${\int }_{0}^{1}{y}^{2}{e}^{-{y}^{2}}dy$。使用分部积分法，设$u={y}^{2}$，$dv={e}^{-{y}^{2}}dy$，则$du=2ydy$，$v=-\frac{1}{2}{e}^{-{y}^{2}}$。因此，${\int }_{0}^{1}{y}^{2}{e}^{-{y}^{2}}dy=-\frac{1}{2}{y}^{2}{e}^{-{y}^{2}}{|}_{0}^{1}+{\int }_{0}^{1}y{e}^{-{y}^{2}}dy$。最后，${\int }_{0}^{1}y{e}^{-{y}^{2}}dy=-\frac{1}{2}{e}^{-{y}^{2}}{|}_{0}^{1}=\frac{1}{2}-\frac{1}{2e}$。

步骤 6：计算最终结果
将所有计算结果代入，得到${\int }_{0}^{1}{\int }_{{x}^{2}}^{1}{x}^{5}{e}^{-{y}^{2}}dydx=\frac{1}{6}[-\frac{1}{2}{e}^{-1}+\frac{3}{2}(\frac{1}{2}-\frac{1}{2e})]=\frac{1}{12}(1-\frac{2}{e})$。