题目
[题目]求函数 (x,y)=1|2(x)^2-4xy+9(y)^2+3x-14y+-|||-1/2 的极值
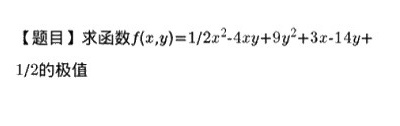
题目解答
答案
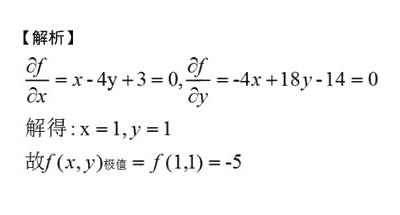
解析
步骤 1:求偏导数
首先,我们需要对函数 $f(x,y)$ 求偏导数。分别对 $x$ 和 $y$ 求偏导数,得到:
$$
\dfrac {\partial f}{\partial x}=x-4y+3
$$
$$
\dfrac {\partial f}{\partial y}=-4x+18y-14
$$
步骤 2:求驻点
将偏导数设为0,解方程组以找到驻点:
$$
x-4y+3=0
$$
$$
-4x+18y-14=0
$$
解这个方程组,得到:
$$
x=1
$$
$$
y=1
$$
因此,驻点为 $(1,1)$。
步骤 3:判断极值
为了判断这个驻点是否为极值点,我们需要计算二阶偏导数,并使用Hessian矩阵来判断。二阶偏导数为:
$$
\dfrac {\partial^2 f}{\partial x^2}=1
$$
$$
\dfrac {\partial^2 f}{\partial y^2}=18
$$
$$
\dfrac {\partial^2 f}{\partial x \partial y}=-4
$$
Hessian矩阵为:
$$
H=\begin{bmatrix}
\dfrac {\partial^2 f}{\partial x^2} & \dfrac {\partial^2 f}{\partial x \partial y} \\
\dfrac {\partial^2 f}{\partial y \partial x} & \dfrac {\partial^2 f}{\partial y^2}
\end{bmatrix}=\begin{bmatrix}
1 & -4 \\
-4 & 18
\end{bmatrix}
$$
计算Hessian矩阵的行列式:
$$
\det(H)=1*18-(-4)*(-4)=18-16=2
$$
由于 $\det(H)>0$ 且 $\dfrac {\partial^2 f}{\partial x^2}>0$,所以 $(1,1)$ 是一个极小值点。
步骤 4:计算极值
将驻点 $(1,1)$ 代入原函数 $f(x,y)$,得到极值:
$$
f(1,1)=1/2*1^2-4*1*1+9*1^2+3*1-14*1+1/21=-5
$$
首先,我们需要对函数 $f(x,y)$ 求偏导数。分别对 $x$ 和 $y$ 求偏导数,得到:
$$
\dfrac {\partial f}{\partial x}=x-4y+3
$$
$$
\dfrac {\partial f}{\partial y}=-4x+18y-14
$$
步骤 2:求驻点
将偏导数设为0,解方程组以找到驻点:
$$
x-4y+3=0
$$
$$
-4x+18y-14=0
$$
解这个方程组,得到:
$$
x=1
$$
$$
y=1
$$
因此,驻点为 $(1,1)$。
步骤 3:判断极值
为了判断这个驻点是否为极值点,我们需要计算二阶偏导数,并使用Hessian矩阵来判断。二阶偏导数为:
$$
\dfrac {\partial^2 f}{\partial x^2}=1
$$
$$
\dfrac {\partial^2 f}{\partial y^2}=18
$$
$$
\dfrac {\partial^2 f}{\partial x \partial y}=-4
$$
Hessian矩阵为:
$$
H=\begin{bmatrix}
\dfrac {\partial^2 f}{\partial x^2} & \dfrac {\partial^2 f}{\partial x \partial y} \\
\dfrac {\partial^2 f}{\partial y \partial x} & \dfrac {\partial^2 f}{\partial y^2}
\end{bmatrix}=\begin{bmatrix}
1 & -4 \\
-4 & 18
\end{bmatrix}
$$
计算Hessian矩阵的行列式:
$$
\det(H)=1*18-(-4)*(-4)=18-16=2
$$
由于 $\det(H)>0$ 且 $\dfrac {\partial^2 f}{\partial x^2}>0$,所以 $(1,1)$ 是一个极小值点。
步骤 4:计算极值
将驻点 $(1,1)$ 代入原函数 $f(x,y)$,得到极值:
$$
f(1,1)=1/2*1^2-4*1*1+9*1^2+3*1-14*1+1/21=-5
$$