题目
已知旋转曲面的方程为 =1-(x)^2-(y)^2-|||-(2geqslant 0),-|||-(1)指出形成旋转曲面的平面曲线及旋转轴;-|||-(2)若曲面取上侧,计算曲面积-|||-=iint (x+1)dydz-ydzdx+(z)^2dxdy
题目解答
答案
解：
（1）画出曲面图像为
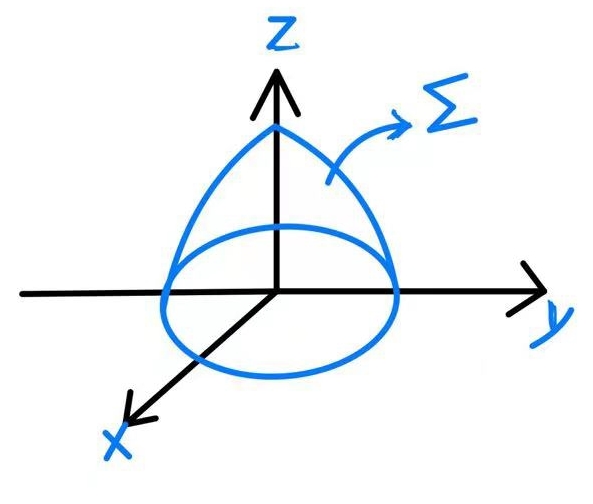
令z=0，则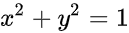
即为平面图形，
由图像知曲面绕z轴旋转。
解析
步骤 1：确定旋转曲面的平面曲线及旋转轴
旋转曲面的方程为 $z=1-{x}^{2}-{y}^{2}$，这是一个以z轴为中心轴的旋转抛物面。当z=0时，方程变为${x}^{2}+{y}^{2}=1$，这是一个半径为1的圆。因此，旋转曲面是由这个圆绕z轴旋转形成的。
步骤 2：计算曲面积分
曲面积分 $I=\iint (x+1)dydz-ydzdx+{z}^{2}dxdy$，其中曲面取上侧。为了计算这个积分，我们使用高斯公式（散度定理）。
首先，计算向量场$\vec{F}=(x+1,-y,z^2)$的散度：
$$\nabla \cdot \vec{F} = \frac{\partial (x+1)}{\partial x} + \frac{\partial (-y)}{\partial y} + \frac{\partial (z^2)}{\partial z} = 1 - 1 + 2z = 2z$$
然后，根据高斯公式，曲面积分可以转化为体积积分：
$$I = \iiint_V 2z \, dV$$
其中，$V$是旋转曲面$z=1-x^2-y^2$和$z=0$之间的体积。为了计算这个体积积分，我们使用柱坐标系，其中$x=r\cos\theta$，$y=r\sin\theta$，$z=z$，$dV=r\,dr\,d\theta\,dz$。积分的范围是$0\leq r\leq 1$，$0\leq \theta\leq 2\pi$，$0\leq z\leq 1-r^2$。因此，体积积分为：
$$I = \int_0^{2\pi} \int_0^1 \int_0^{1-r^2} 2zr \, dz \, dr \, d\theta$$
计算这个积分，我们得到：
$$I = \int_0^{2\pi} \int_0^1 r \left[ z^2 \right]_0^{1-r^2} \, dr \, d\theta = \int_0^{2\pi} \int_0^1 r(1-r^2)^2 \, dr \, d\theta$$
$$I = \int_0^{2\pi} \int_0^1 r(1-2r^2+r^4) \, dr \, d\theta = \int_0^{2\pi} \left[ \frac{r^2}{2} - \frac{2r^4}{4} + \frac{r^6}{6} \right]_0^1 \, d\theta$$
$$I = \int_0^{2\pi} \left( \frac{1}{2} - \frac{1}{2} + \frac{1}{6} \right) \, d\theta = \int_0^{2\pi} \frac{1}{6} \, d\theta = \frac{1}{6} \cdot 2\pi = \frac{\pi}{3}$$
旋转曲面的方程为 $z=1-{x}^{2}-{y}^{2}$，这是一个以z轴为中心轴的旋转抛物面。当z=0时，方程变为${x}^{2}+{y}^{2}=1$，这是一个半径为1的圆。因此，旋转曲面是由这个圆绕z轴旋转形成的。
步骤 2：计算曲面积分
曲面积分 $I=\iint (x+1)dydz-ydzdx+{z}^{2}dxdy$，其中曲面取上侧。为了计算这个积分，我们使用高斯公式（散度定理）。
首先，计算向量场$\vec{F}=(x+1,-y,z^2)$的散度：
$$\nabla \cdot \vec{F} = \frac{\partial (x+1)}{\partial x} + \frac{\partial (-y)}{\partial y} + \frac{\partial (z^2)}{\partial z} = 1 - 1 + 2z = 2z$$
然后，根据高斯公式，曲面积分可以转化为体积积分：
$$I = \iiint_V 2z \, dV$$
其中，$V$是旋转曲面$z=1-x^2-y^2$和$z=0$之间的体积。为了计算这个体积积分，我们使用柱坐标系，其中$x=r\cos\theta$，$y=r\sin\theta$，$z=z$，$dV=r\,dr\,d\theta\,dz$。积分的范围是$0\leq r\leq 1$，$0\leq \theta\leq 2\pi$，$0\leq z\leq 1-r^2$。因此，体积积分为：
$$I = \int_0^{2\pi} \int_0^1 \int_0^{1-r^2} 2zr \, dz \, dr \, d\theta$$
计算这个积分，我们得到：
$$I = \int_0^{2\pi} \int_0^1 r \left[ z^2 \right]_0^{1-r^2} \, dr \, d\theta = \int_0^{2\pi} \int_0^1 r(1-r^2)^2 \, dr \, d\theta$$
$$I = \int_0^{2\pi} \int_0^1 r(1-2r^2+r^4) \, dr \, d\theta = \int_0^{2\pi} \left[ \frac{r^2}{2} - \frac{2r^4}{4} + \frac{r^6}{6} \right]_0^1 \, d\theta$$
$$I = \int_0^{2\pi} \left( \frac{1}{2} - \frac{1}{2} + \frac{1}{6} \right) \, d\theta = \int_0^{2\pi} \frac{1}{6} \, d\theta = \frac{1}{6} \cdot 2\pi = \frac{\pi}{3}$$