题目
计算曲面积分iint (z+2x+dfrac (4)(3)y)ds-|||-__,其中曲面iint (z+2x+dfrac (4)(3)y)ds-|||-__以iint (z+2x+dfrac (4)(3)y)ds-|||-__为顶点的三角形平面区域。
计算曲面积分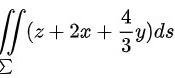 ,其中曲面
,其中曲面 以
以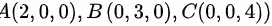 为顶点的三角形平面区域。
为顶点的三角形平面区域。
题目解答
答案
三角形区域如下:
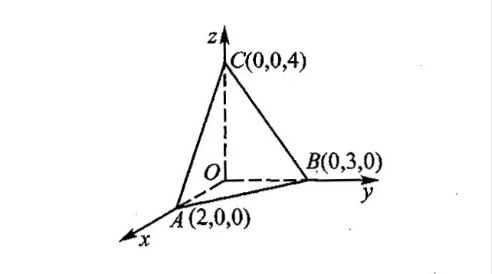
则:
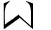 的方程为
的方程为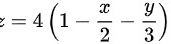 , 它在
, 它在
 平面上的投影区域
平面上的投影区域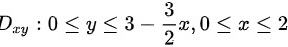 。
。
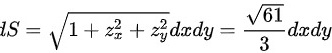
故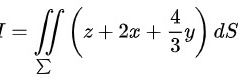
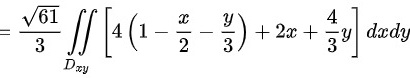
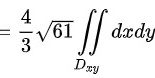
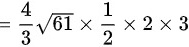
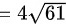
∴本题答案为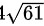 。
。
解析
步骤 1:确定曲面方程
根据题目中给出的三个顶点A(2,0,0), B(0,3,0), C(0,0,4),可以确定曲面方程。首先,通过这三个点可以确定平面方程。设平面方程为$z = ax + by + c$,将三个点代入方程中,可以解出$a$、$b$、$c$的值。将A(2,0,0)代入得$0 = 2a + c$,将B(0,3,0)代入得$0 = 3b + c$,将C(0,0,4)代入得$4 = c$。解得$a = -2$,$b = -\dfrac{4}{3}$,$c = 4$。因此,平面方程为$z = -2x - \dfrac{4}{3}y + 4$。
步骤 2:确定投影区域
曲面在xoy平面上的投影区域为三角形区域,顶点为A(2,0,0), B(0,3,0)。投影区域的边界方程为$y = 3 - \dfrac{3}{2}x$,$0 \leqslant x \leqslant 2$,$0 \leqslant y \leqslant 3 - \dfrac{3}{2}x$。
步骤 3:计算曲面积分
曲面积分$\iint (x+2x+\dfrac {4}{3}y)ds$可以转化为二重积分$\iint (x+2x+\dfrac {4}{3}y)\sqrt{1+{z_x}^2+{z_y}^2}dxdy$。其中,$z_x = -2$,$z_y = -\dfrac{4}{3}$,$\sqrt{1+{z_x}^2+{z_y}^2} = \sqrt{1+4+\dfrac{16}{9}} = \dfrac{\sqrt{61}}{3}$。因此,曲面积分可以转化为$\dfrac{\sqrt{61}}{3}\iint (x+2x+\dfrac {4}{3}y)dxdy$。将平面方程代入,得$\dfrac{\sqrt{61}}{3}\iint [4(1-\dfrac{x}{2}-\dfrac{y}{3})+2x+\dfrac{4}{3}y]dxdy$。计算二重积分,得$4\sqrt{61}$。
根据题目中给出的三个顶点A(2,0,0), B(0,3,0), C(0,0,4),可以确定曲面方程。首先,通过这三个点可以确定平面方程。设平面方程为$z = ax + by + c$,将三个点代入方程中,可以解出$a$、$b$、$c$的值。将A(2,0,0)代入得$0 = 2a + c$,将B(0,3,0)代入得$0 = 3b + c$,将C(0,0,4)代入得$4 = c$。解得$a = -2$,$b = -\dfrac{4}{3}$,$c = 4$。因此,平面方程为$z = -2x - \dfrac{4}{3}y + 4$。
步骤 2:确定投影区域
曲面在xoy平面上的投影区域为三角形区域,顶点为A(2,0,0), B(0,3,0)。投影区域的边界方程为$y = 3 - \dfrac{3}{2}x$,$0 \leqslant x \leqslant 2$,$0 \leqslant y \leqslant 3 - \dfrac{3}{2}x$。
步骤 3:计算曲面积分
曲面积分$\iint (x+2x+\dfrac {4}{3}y)ds$可以转化为二重积分$\iint (x+2x+\dfrac {4}{3}y)\sqrt{1+{z_x}^2+{z_y}^2}dxdy$。其中,$z_x = -2$,$z_y = -\dfrac{4}{3}$,$\sqrt{1+{z_x}^2+{z_y}^2} = \sqrt{1+4+\dfrac{16}{9}} = \dfrac{\sqrt{61}}{3}$。因此,曲面积分可以转化为$\dfrac{\sqrt{61}}{3}\iint (x+2x+\dfrac {4}{3}y)dxdy$。将平面方程代入,得$\dfrac{\sqrt{61}}{3}\iint [4(1-\dfrac{x}{2}-\dfrac{y}{3})+2x+\dfrac{4}{3}y]dxdy$。计算二重积分,得$4\sqrt{61}$。