题目
设 ^2+(y)^2+(z)^2-4z=0, 求 dfrac ({a)^2z}(q{x)^2}
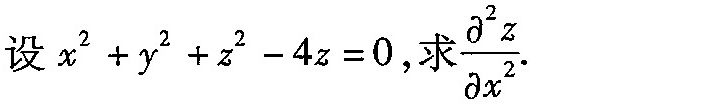
题目解答
答案
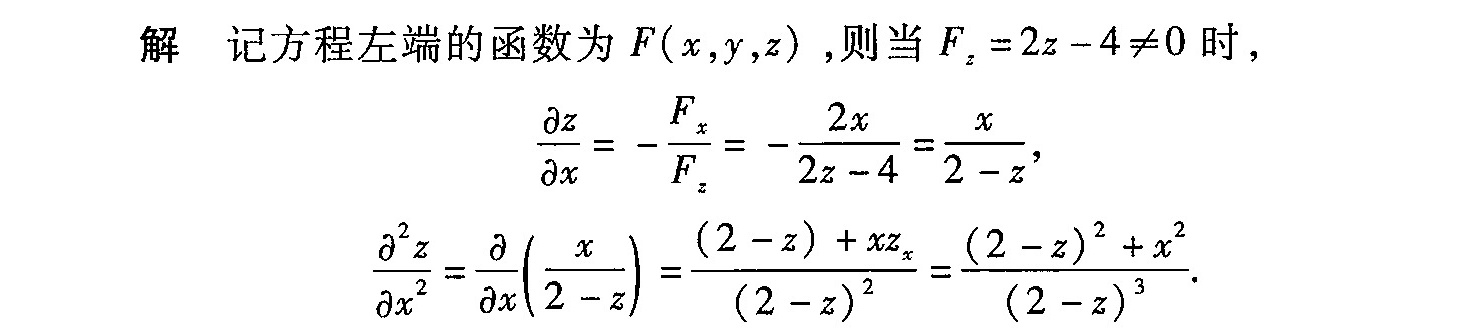
解析
步骤 1:定义函数
定义函数 $F(x,y,z) = x^2 + y^2 + z^2 - 4z$,根据题目条件,我们需要求解 $\dfrac{{\partial}^2 z}{\partial x^2}$。
步骤 2:隐函数求导
根据隐函数求导法则,当 ${F}_{z} \neq 0$ 时,有 $\dfrac{\partial z}{\partial x} = -\dfrac{{F}_{x}}{{F}_{z}}$。首先计算 ${F}_{x}$ 和 ${F}_{z}$。
- ${F}_{x} = 2x$
- ${F}_{z} = 2z - 4$
步骤 3:计算一阶偏导数
代入 ${F}_{x}$ 和 ${F}_{z}$,得到 $\dfrac{\partial z}{\partial x} = -\dfrac{2x}{2z-4} = \dfrac{x}{2-z}$。
步骤 4:计算二阶偏导数
接下来,计算 $\dfrac{{\partial}^2 z}{\partial x^2}$,即对 $\dfrac{\partial z}{\partial x}$ 关于 $x$ 再次求导。
- $\dfrac{{\partial}^2 z}{\partial x^2} = \dfrac{\partial}{\partial x}(\dfrac{x}{2-z}) = \dfrac{(2-z) - x(-\dfrac{\partial z}{\partial x})}{(2-z)^2}$
- 代入 $\dfrac{\partial z}{\partial x} = \dfrac{x}{2-z}$,得到 $\dfrac{{\partial}^2 z}{\partial x^2} = \dfrac{(2-z) + x(\dfrac{x}{2-z})}{(2-z)^2} = \dfrac{(2-z)^2 + x^2}{(2-z)^3}$
定义函数 $F(x,y,z) = x^2 + y^2 + z^2 - 4z$,根据题目条件,我们需要求解 $\dfrac{{\partial}^2 z}{\partial x^2}$。
步骤 2:隐函数求导
根据隐函数求导法则,当 ${F}_{z} \neq 0$ 时,有 $\dfrac{\partial z}{\partial x} = -\dfrac{{F}_{x}}{{F}_{z}}$。首先计算 ${F}_{x}$ 和 ${F}_{z}$。
- ${F}_{x} = 2x$
- ${F}_{z} = 2z - 4$
步骤 3:计算一阶偏导数
代入 ${F}_{x}$ 和 ${F}_{z}$,得到 $\dfrac{\partial z}{\partial x} = -\dfrac{2x}{2z-4} = \dfrac{x}{2-z}$。
步骤 4:计算二阶偏导数
接下来,计算 $\dfrac{{\partial}^2 z}{\partial x^2}$,即对 $\dfrac{\partial z}{\partial x}$ 关于 $x$ 再次求导。
- $\dfrac{{\partial}^2 z}{\partial x^2} = \dfrac{\partial}{\partial x}(\dfrac{x}{2-z}) = \dfrac{(2-z) - x(-\dfrac{\partial z}{\partial x})}{(2-z)^2}$
- 代入 $\dfrac{\partial z}{\partial x} = \dfrac{x}{2-z}$,得到 $\dfrac{{\partial}^2 z}{\partial x^2} = \dfrac{(2-z) + x(\dfrac{x}{2-z})}{(2-z)^2} = \dfrac{(2-z)^2 + x^2}{(2-z)^3}$