1.5 将圆周方程 ((x)^2+(y)^2)+bx+cy+d=0 (aneq 0) 写成复数形式(即用z-|||-与z来表示,其中 =x+iy).
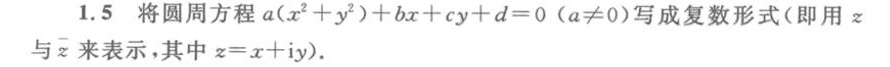
题目解答
答案
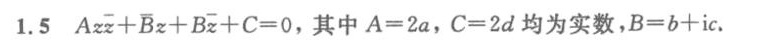
解析
考查要点:本题主要考查将圆的一般方程转化为复数形式的能力,需要理解复数与平面坐标的关系,以及如何利用复数及其共轭表示几何图形。
解题核心思路:
- 复数与坐标系的对应:复数$z = x + iy$对应平面上的点$(x, y)$,其共轭复数$\overline{z} = x - iy$。
- 模长平方的表示:$z\overline{z} = x^2 + y^2$,可替代原方程中的$x^2 + y^2$项。
- 线性项的复数表示:通过构造复数$B = b + ic$,利用$B\overline{z} + \overline{B}z$表示$bx + cy$,并提取其实部。
- 方程整体调整:通过系数调整,将原方程转化为标准复数形式。
破题关键点:
- 识别$x^2 + y^2$的复数形式:直接对应$z\overline{z}$。
- 构造复数$B$:将$bx + cy$转化为$B\overline{z} + \overline{B}z$,其中$B = b + ic$。
- 系数匹配:通过方程两边乘以2,统一各项系数,得到最终形式。
将原方程$a(x^2 + y^2) + bx + cy + d = 0$逐步转换为复数形式:
步骤1:处理$x^2 + y^2$项
利用$z\overline{z} = x^2 + y^2$,原方程中的$a(x^2 + y^2)$可表示为:
$a \cdot z\overline{z}$
根据题目答案,需引入系数$A = 2a$,因此调整为:
$A \cdot z\overline{z} \quad \text{其中} \quad A = 2a$
步骤2:处理线性项$bx + cy$
构造复数$B = b + ic$,其共轭为$\overline{B} = b - ic$。通过计算:
$B\overline{z} + \overline{B}z = (b + ic)(x - iy) + (b - ic)(x + iy)$
展开后虚部抵消,实部为:
$2bx + 2cy \quad \Rightarrow \quad bx + cy = \frac{B\overline{z} + \overline{B}z}{2}$
为匹配原方程,需将系数调整为1,因此整体方程乘以2。
步骤3:整合常数项
原方程中的常数项$d$对应复数形式中的$C$,根据题目答案需令$C = 2d$,因此调整为:
$C \quad \text{其中} \quad C = 2d$
步骤4:组合所有项
将调整后的各项代入原方程并整理:
$2a \cdot z\overline{z} + (B\overline{z} + \overline{B}z) + 2d = 0$
即:
$Az\overline{z} + \overline{B}z + B\overline{z} + C = 0$
其中$A = 2a$,$C = 2d$,$B = b + ic$。