题目
[题目]设 (x)=((dfrac {1)(x))}^x+(x)^2x, 求f(x).
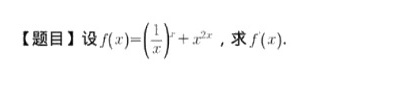
题目解答
答案

解析
本题要求求函数 $f(x) = \left(\dfrac{1}{x}\right)^x + x^{2x}$ 的导数 $f'(x)$。核心思路是对两个项分别求导后相加,每个项均需使用对数求导法处理指数函数。关键点在于正确应用链式法则和乘积法则,特别注意符号和化简过程。
第一项 $\left(\dfrac{1}{x}\right)^x$ 的导数
- 表达式变形:$\left(\dfrac{1}{x}\right)^x = x^{-x} = e^{-x \ln x}$。
- 对数求导:设 $y = e^{-x \ln x}$,则 $\ln y = -x \ln x$。
- 求导并化简:
- 对两边求导:$\dfrac{1}{y} \cdot y' = -(\ln x + 1)$。
- 解得:$y' = -x^{-x} (\ln x + 1) = -\left(\dfrac{1}{x}\right)^x (\ln x + 1)$。
第二项 $x^{2x}$ 的导数
- 对数求导:设 $y = x^{2x}$,则 $\ln y = 2x \ln x$。
- 求导并化简:
- 对两边求导:$\dfrac{1}{y} \cdot y' = 2(\ln x + 1)$。
- 解得:$y' = x^{2x} \cdot 2(\ln x + 1) = 2x^{2x} (\ln x + 1)$。
合并结果
将两部分导数相加:
$f'(x) = -\left(\dfrac{1}{x}\right)^x (\ln x + 1) + 2x^{2x} (\ln x + 1)$