利用导数证明:当 gt 1 时, dfrac (ln (1+x))(ln x)gt dfrac (x)(1+x)
题目解答
答案
解析: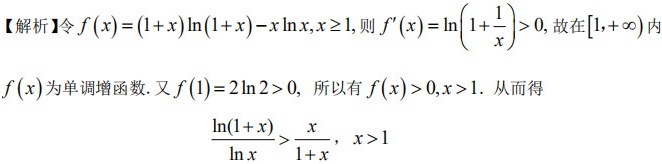
解析
考查要点:本题主要考查利用导数证明不等式的方法,涉及函数构造、导数求解及单调性分析。
解题核心思路:
- 构造辅助函数:将不等式变形为$f(x) = (1+x)\ln(1+x) - x\ln x$,转化为证明$f(x) > 0$($x > 1$)。
- 分析函数单调性:通过求导$f'(x)$,判断$f(x)$在$x \geq 1$时的单调性。
- 结合初始值:验证$f(1) > 0$,结合单调性得出$f(x) > 0$在$x > 1$时恒成立。
破题关键点:
- 正确构造函数是关键,需将不等式转化为易于分析的形式。
- 导数的符号判断直接影响单调性结论,需准确计算$f'(x)$并分析其正负。
步骤1:构造辅助函数
将原不等式$\dfrac{\ln(1+x)}{\ln x} > \dfrac{x}{1+x}$变形为:
$(1+x)\ln(1+x) > x\ln x.$
定义函数$f(x) = (1+x)\ln(1+x) - x\ln x$,需证明$f(x) > 0$($x > 1$)。
步骤2:求导分析单调性
计算$f(x)$的导数:
$\begin{aligned}f'(x) &= \frac{d}{dx}\left[(1+x)\ln(1+x)\right] - \frac{d}{dx}\left[x\ln x\right] \\&= \ln(1+x) + \frac{1+x}{1+x} - \ln x - \frac{x}{x} \\&= \ln(1+x) + 1 - \ln x - 1 \\&= \ln\left(1 + \frac{1}{x}\right).\end{aligned}$
关键结论:当$x \geq 1$时,$\dfrac{1}{x} \leq 1$,故$1 + \dfrac{1}{x} > 1$,因此$f'(x) = \ln\left(1 + \dfrac{1}{x}\right) > 0$,说明$f(x)$在$[1, +\infty)$上单调递增。
步骤3:验证初始值
计算$f(1)$:
$f(1) = (1+1)\ln(1+1) - 1 \cdot \ln 1 = 2\ln 2 > 0.$
结合单调性:由于$f(x)$在$x \geq 1$时单调递增且$f(1) > 0$,故当$x > 1$时,$f(x) > f(1) > 0$,即原不等式成立。