题目
求函数=((dfrac {1)(1+x))}^x的导数。
求函数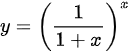 的导数。
的导数。
题目解答
答案
本题考查了复合函数的求导。
分析:先把原函数表达式换成以e为底的指数形式,接着用复合函数求导法则求导即可解答。
解: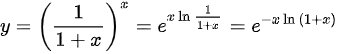
根据复合函数求导法则,则
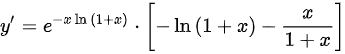
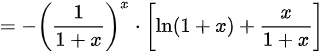 。
。
故答案为: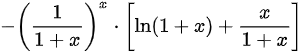 。
。
解析
步骤 1:转换函数形式
将原函数$y={(\dfrac {1}{1+x})}^{x}$转换为以$e$为底的指数形式,即$y={e}^{x\ln \dfrac {1}{1+x}}={e}^{-x\ln (1+x)}$。
步骤 2:应用复合函数求导法则
根据复合函数求导法则,对$y={e}^{-x\ln (1+x)}$求导,得到$y'={e}^{-x\ln (1+x)}\cdot [-\ln (1+x)-\dfrac {x}{1+x}]$。
步骤 3:简化导数表达式
将导数表达式简化为$y'=-{(\dfrac {1}{1+x})}^{x}\cdot [ \ln (1+x)+\dfrac {x}{1+x}] $。
将原函数$y={(\dfrac {1}{1+x})}^{x}$转换为以$e$为底的指数形式,即$y={e}^{x\ln \dfrac {1}{1+x}}={e}^{-x\ln (1+x)}$。
步骤 2:应用复合函数求导法则
根据复合函数求导法则,对$y={e}^{-x\ln (1+x)}$求导,得到$y'={e}^{-x\ln (1+x)}\cdot [-\ln (1+x)-\dfrac {x}{1+x}]$。
步骤 3:简化导数表达式
将导数表达式简化为$y'=-{(\dfrac {1}{1+x})}^{x}\cdot [ \ln (1+x)+\dfrac {x}{1+x}] $。