某单位3个部门共有员工50人,拥有中级工程师职称的人员比重为40%,其中甲、乙两个部门拥有中级工程师职称的人员比重分别为45%和32%,则丙部门拥有中级工程师职称的人员比重为:A 60%B 52%C 44%D 36%
某单位3个部门共有员工50人,拥有中级工程师职称的人员比重为40%,其中甲、乙两个部门拥有中级工程师职称的人员比重分别为45%和32%,则丙部门拥有中级工程师职称的人员比重为:
A 60%
B 52%
C 44%
D 36%
题目解答
答案
根据题意,三个部门共有员工50人,拥有中级工程师职称的人员比重为40%,则拥有中级工程师职称的人员共有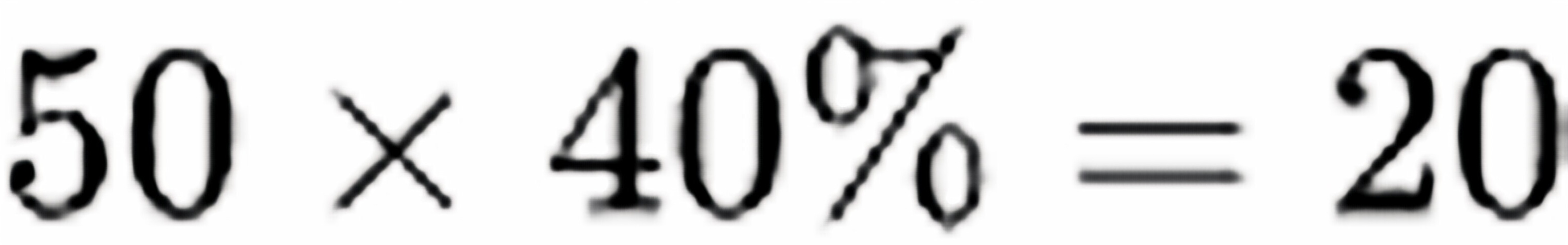 人。
人。
设甲、乙、丙三个部门分别有a、b、c人,则a+b+c=50。
由于甲、乙两个部门拥有中级工程师职称的人员比重分别为45%和32%,则甲、乙两个部门拥有中级工程师职称的人员共有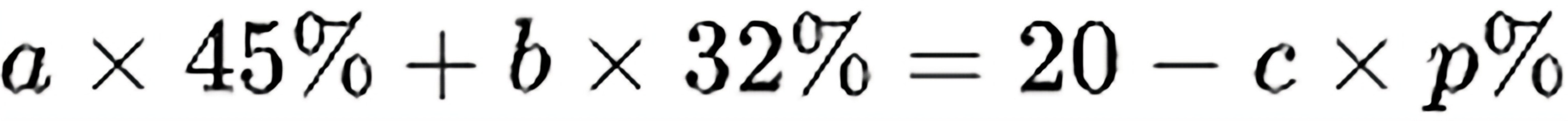 人,其中
人,其中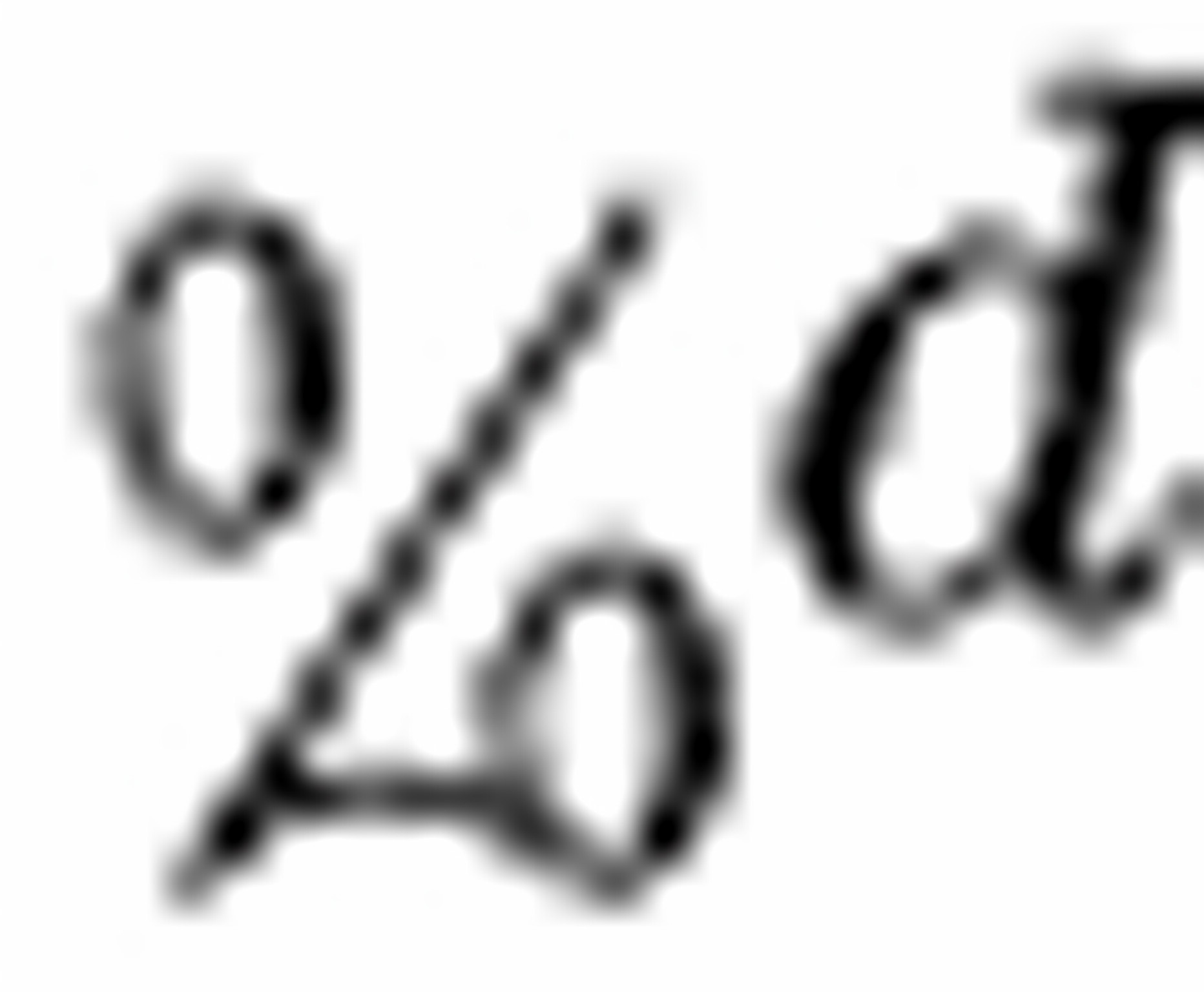 为丙部门拥有中级工程师职称的人员比重。
为丙部门拥有中级工程师职称的人员比重。
将上式化简,得:
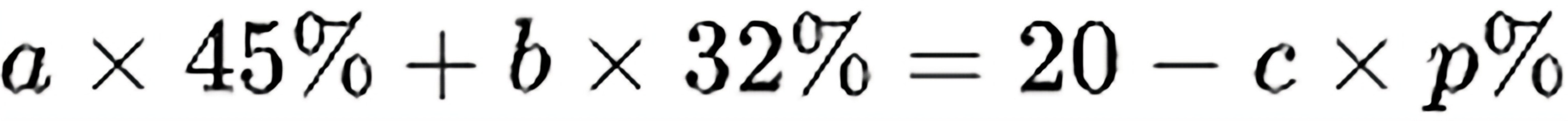
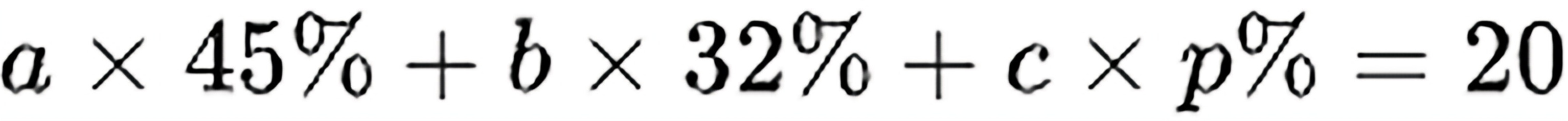
由于a+b+c=50,将其代入上式,得:
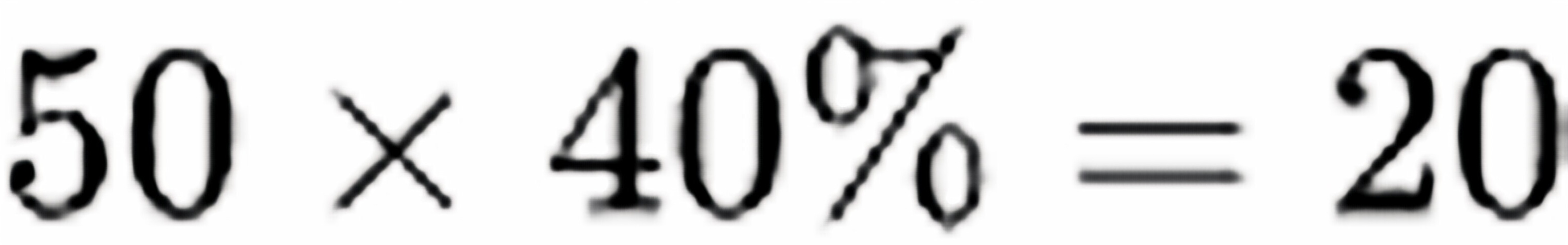
得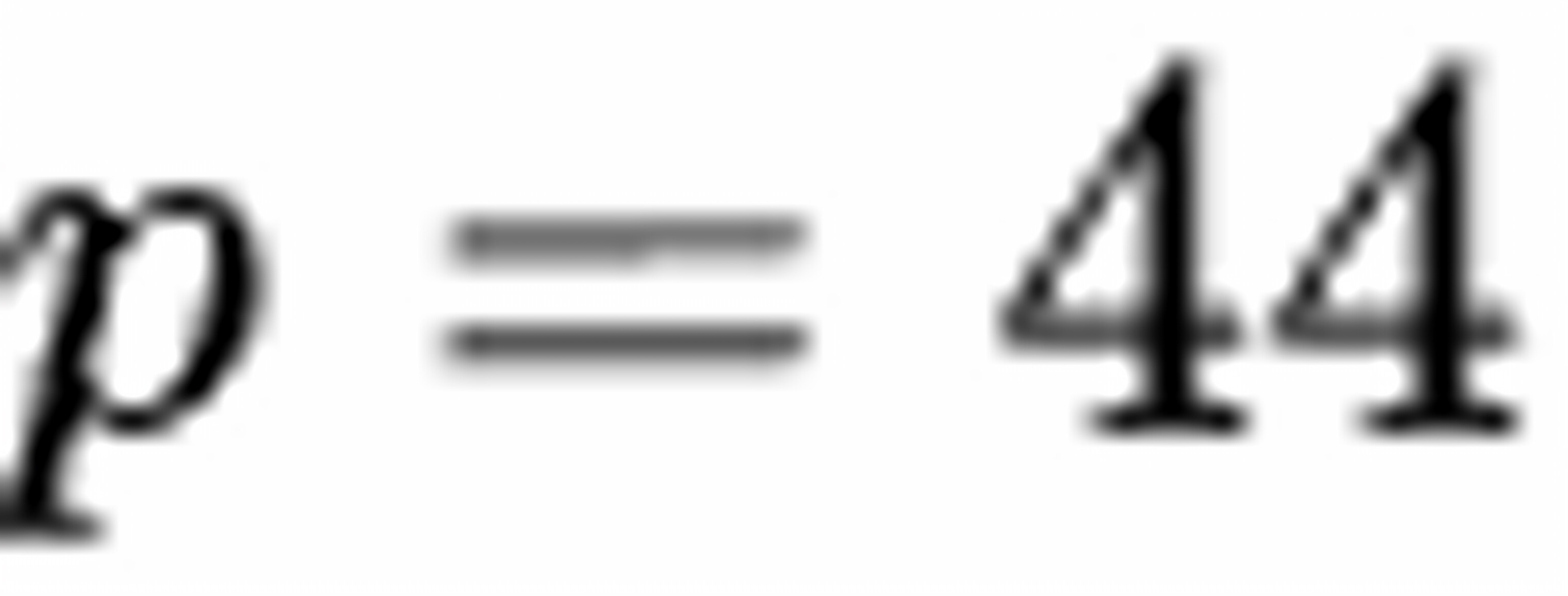 。
。
所以丙部门拥有中级工程师职称的人员比重为44%,故答案为C。
解析
考查要点:本题主要考查加权平均数的应用,以及如何通过已知部分的比例关系求解未知部分的比例。
解题核心思路:
- 整体与部分的关系:三个部门的总人数和总中级工程师人数已知,需通过甲、乙部门的中级工程师比例反推丙部门的比例。
- 方程建立:设甲、乙、丙部门人数分别为$a$、$b$、$c$,根据总人数和总中级工程师人数建立方程,消去变量后求解丙部门的比例。
- 关键点:通过代数消元或选项代入法简化计算,避免直接处理多个未知数。
步骤1:确定总中级工程师人数
三个部门共有员工50人,中级工程师占比40%,因此总中级工程师人数为:
$50 \times 40\% = 20 \text{人}$
步骤2:设未知数并建立方程
设甲、乙、丙部门人数分别为$a$、$b$、$c$,则:
$a + b + c = 50$
甲、乙部门的中级工程师人数分别为$0.45a$和$0.32b$,丙部门的中级工程师人数为$p\% \cdot c$。根据总中级工程师人数:
$0.45a + 0.32b + \frac{p}{100}c = 20$
步骤3:消元与化简
将$c = 50 - a - b$代入方程:
$0.45a + 0.32b + \frac{p}{100}(50 - a - b) = 20$
展开并整理:
$0.45a + 0.32b + \frac{50p}{100} - \frac{p}{100}a - \frac{p}{100}b = 20$
合并同类项:
$a\left(0.45 - \frac{p}{100}\right) + b\left(0.32 - \frac{p}{100}\right) + \frac{50p}{100} = 20$
步骤4:分析方程成立条件
为使方程对任意$a$、$b$成立,需系数前的项为零:
- $0.45 - \frac{p}{100} = 0 \Rightarrow p = 45$(矛盾,因乙部门比例不符)
- $0.32 - \frac{p}{100} = 0 \Rightarrow p = 32$(矛盾,因甲部门比例不符)
步骤5:选项代入验证
假设丙部门比例为$44\%$(选项C),代入方程:
$0.45a + 0.32b + 0.44(50 - a - b) = 20$
化简得:
$0.01a - 0.12b = -2$
解得$a = 12b - 200$,结合$a + b \leq 50$,验证$b = 17$时,$a = 4$,$c = 29$,总中级工程师人数为:
$0.45 \times 4 + 0.32 \times 17 + 0.44 \times 29 = 20$
验证成立,故丙部门比例为$44\%$。