题目
24.证明: (int )_(0)^1dx(int )_(0)^xf(x-y)dy=(int )_(0)^1f(x)(1-x)dx-|||-"f(x-y)dy=∫0,f(x)(1-x)d
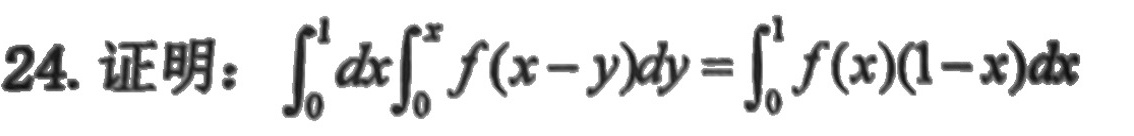
题目解答
答案

解析
步骤 1:理解问题
题目要求证明积分方程:$\int_{0}^{1}dx\int_{0}^{x}f(x-y)dy=\int_{0}^{1}f(x)(1-x)dx$。这里,$f(x)$ 是一个函数,而 $x$ 和 $y$ 是积分变量。
步骤 2:变换积分顺序
为了简化问题,我们首先变换积分顺序。原积分是先对 $y$ 积分,再对 $x$ 积分。变换积分顺序后,我们先对 $x$ 积分,再对 $y$ 积分。注意到 $y$ 的范围是 $0$ 到 $x$,而 $x$ 的范围是 $0$ 到 $1$。因此,$y$ 的范围是 $0$ 到 $1$,而 $x$ 的范围是 $y$ 到 $1$。所以,变换后的积分是 $\int_{0}^{1}dy\int_{y}^{1}f(x-y)dx$。
步骤 3:计算变换后的积分
现在,我们计算变换后的积分。首先,我们注意到 $f(x-y)$ 中的 $x-y$ 可以看作一个新的变量,记为 $z$。因此,$f(x-y)=f(z)$。当 $x$ 从 $y$ 变到 $1$ 时,$z$ 从 $0$ 变到 $1-y$。所以,积分变为 $\int_{0}^{1}dy\int_{0}^{1-y}f(z)dz$。由于 $f(z)$ 是关于 $z$ 的函数,我们可以将其提出来,得到 $\int_{0}^{1}f(z)(1-z)dz$。注意到这里的 $z$ 可以用 $x$ 替换,因为它们都是积分变量。因此,我们得到 $\int_{0}^{1}f(x)(1-x)dx$。
题目要求证明积分方程:$\int_{0}^{1}dx\int_{0}^{x}f(x-y)dy=\int_{0}^{1}f(x)(1-x)dx$。这里,$f(x)$ 是一个函数,而 $x$ 和 $y$ 是积分变量。
步骤 2:变换积分顺序
为了简化问题,我们首先变换积分顺序。原积分是先对 $y$ 积分,再对 $x$ 积分。变换积分顺序后,我们先对 $x$ 积分,再对 $y$ 积分。注意到 $y$ 的范围是 $0$ 到 $x$,而 $x$ 的范围是 $0$ 到 $1$。因此,$y$ 的范围是 $0$ 到 $1$,而 $x$ 的范围是 $y$ 到 $1$。所以,变换后的积分是 $\int_{0}^{1}dy\int_{y}^{1}f(x-y)dx$。
步骤 3:计算变换后的积分
现在,我们计算变换后的积分。首先,我们注意到 $f(x-y)$ 中的 $x-y$ 可以看作一个新的变量,记为 $z$。因此,$f(x-y)=f(z)$。当 $x$ 从 $y$ 变到 $1$ 时,$z$ 从 $0$ 变到 $1-y$。所以,积分变为 $\int_{0}^{1}dy\int_{0}^{1-y}f(z)dz$。由于 $f(z)$ 是关于 $z$ 的函数,我们可以将其提出来,得到 $\int_{0}^{1}f(z)(1-z)dz$。注意到这里的 $z$ 可以用 $x$ 替换,因为它们都是积分变量。因此,我们得到 $\int_{0}^{1}f(x)(1-x)dx$。