题目
设 g(x)= ) 2-x,xleqslant 0 2+x,xgt 0g(f(x))= __ .
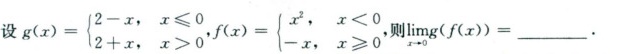
题目解答
答案
解:

解析
步骤 1:确定f(x)的值域
根据f(x)的定义,当 $x\lt 0$ 时,$f(x)={x}^{2}\gt 0$;当 $x\geqslant 0$ 时,$f(x)=-x\leqslant 0$。因此,f(x)的值域为全体实数。
步骤 2:确定g(f(x))的表达式
根据g(x)的定义,当 $f(x)\leqslant 0$ 时,$g(f(x))=2-f(x)$;当 $f(x)\gt 0$ 时,$g(f(x))=2+f(x)$。结合f(x)的定义,可以得到:
- 当 $x\lt 0$ 时,$f(x)={x}^{2}\gt 0$,所以 $g(f(x))=2+f(x)=2+{x}^{2}$;
- 当 $x\geqslant 0$ 时,$f(x)=-x\leqslant 0$,所以 $g(f(x))=2-f(x)=2-(-x)=2+x$。
步骤 3:计算 $\lim _{x\rightarrow 0}g(f(x))$
- 当 $x\rightarrow {0}^{+}$ 时,$g(f(x))=2+x$,所以 $\lim _{x\rightarrow {0}^{+}}g(f(x))=\lim _{x\rightarrow {0}^{+}}(2+x)=2$;
- 当 $x\rightarrow {0}^{-}$ 时,$g(f(x))=2+{x}^{2}$,所以 $\lim _{x\rightarrow {0}^{-}}g(f(x))=\lim _{x\rightarrow {0}^{-}}(2+{x}^{2})=2$。
由于左右极限相等,所以 $\lim _{x\rightarrow 0}g(f(x))=2$。
根据f(x)的定义,当 $x\lt 0$ 时,$f(x)={x}^{2}\gt 0$;当 $x\geqslant 0$ 时,$f(x)=-x\leqslant 0$。因此,f(x)的值域为全体实数。
步骤 2:确定g(f(x))的表达式
根据g(x)的定义,当 $f(x)\leqslant 0$ 时,$g(f(x))=2-f(x)$;当 $f(x)\gt 0$ 时,$g(f(x))=2+f(x)$。结合f(x)的定义,可以得到:
- 当 $x\lt 0$ 时,$f(x)={x}^{2}\gt 0$,所以 $g(f(x))=2+f(x)=2+{x}^{2}$;
- 当 $x\geqslant 0$ 时,$f(x)=-x\leqslant 0$,所以 $g(f(x))=2-f(x)=2-(-x)=2+x$。
步骤 3:计算 $\lim _{x\rightarrow 0}g(f(x))$
- 当 $x\rightarrow {0}^{+}$ 时,$g(f(x))=2+x$,所以 $\lim _{x\rightarrow {0}^{+}}g(f(x))=\lim _{x\rightarrow {0}^{+}}(2+x)=2$;
- 当 $x\rightarrow {0}^{-}$ 时,$g(f(x))=2+{x}^{2}$,所以 $\lim _{x\rightarrow {0}^{-}}g(f(x))=\lim _{x\rightarrow {0}^{-}}(2+{x}^{2})=2$。
由于左右极限相等,所以 $\lim _{x\rightarrow 0}g(f(x))=2$。